Combine as equações polares com os gráficos com os gráficos . Dê os motivos das suas escolhas. (Não use ferramentas gráficas.)
- ;
- ;
Passo 1
Fala ai! Vamos começar esta questão analisando o gráfico.
Podemos substituir valores em , afim de descobrirmos o valor de pela função .
Para
Para
Para
Temos então a representação do gráfico da função.
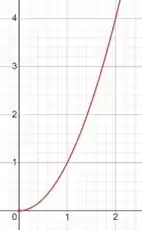
Como podemos ver, começa em e aumenta continuamente. Isso significa que para nossa curva, aumenta conforme aumenta, o que significa que segue uma forma espiral similar aos gráficos e .
Passo 2
Agora que restingimos as opções de gráficos, fica mais fácil.
Vamos lá... Sabemos que:
- A equação ² descreve uma espiral que se expande de forma mais rápida à medida que aumenta. Conforme varia de a , o raio aumenta proporcionalmente ao quadrado do ângulo.
- Observando o gráfico , vemos uma espiral que se expande rapidamente e mantém uma forma claramente definida. A espiral começa a partir da origem e se estende para fora, correspondendo à forma esperada da função com o domínio dado.
Vamos começar desenhando o gráfico de usando o intervalo dado,
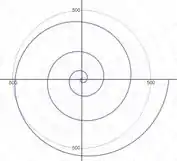
Como cresce bem devagar depois de , como uma típica função logarítmica, o gráfico seria o mais adequado para . Assim, por eliminação, o gráfico é o da função .
indo até significaria que existem 4 voltas ao redor do polo, que seria outro modo de dizer que o gráfico é o correto se pudéssemos ver a curva completa (o que não acontece no caso da figura que tem no livro, já que não conseguimos ver a primeira volta!).
Resposta
O Gráfico correspondente é o .