Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.6 - Ex. 23
Mostre que uma cônica com foco na origem, excentricidade e diretriz tem a equação polar
Passo 1
Hey, galera! Tudo tranquilo?
Vamos começar entendendo o que pode ser feito para resolvermos esta questão.
Para fazer o que foi pedido primeiro vamos construir a curva em questão, iremos também considerar a definição da excentricidade em termos da distância focal da diretriz até o foco. Como a equação da definição já foi dada no enunciado, temos então que analisar apenas.
Passo 2
Bom, pessoal. Primeiro, vamos fazer um esboço do que seria uma cônica com foco na origem, excentricidade e diretriz , beleza?
A equação da diretriz indica que a distância como , onde a é o semieixo maior da dônica. Os pontos (2, 0) e (-2, 0) são interceptados pela curva devido às propriedades da equação polar em e , onde o valor de é calculado para satisfazer as coordenadas cartesianas especificadas. A relação entre 𝑒e, 𝑑d e os valores de determina esses pontos de interseção.
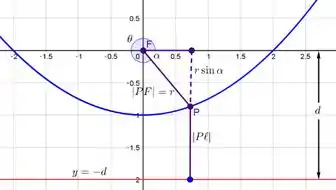
Agora, como provar que essa cônica tem a seguinte equação?
Passo 3
Galera, vamos lembrar de como definimos uma cônica: a razão entre a distância de um ponto qualquer da cônica ao foco e a distância entre esse ponto e a reta diretriz deve ser igual à excentricidade:
Digamos que o ponto tem coordenadas polares e retangulares .
Como mostra a figura, o foco está na origem, então .
Olhando novamente pra figura, vemos que
Como é negativo:
Passo 4
Agora que já temos e em coordenadas polares, jogamos esses valores na equação:
Chegamos onde queríamos, beleza?
Resposta
Demonstração