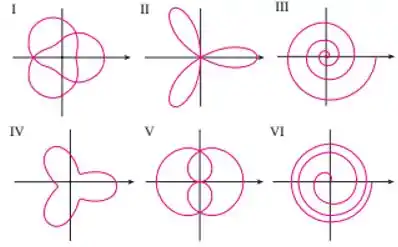
Combine as equações polares com os gráficos com os gráficos . Dê os motivos das suas escolhas. (Não use ferramentas gráficas.)
- ;
- ;
Passo 1
Fala galerinha!
Para encontrarmos o gráfico correto referente a está função, vamos analisar como pode ser o seu comportamente. Mas primeiro vamos relembrar como é o gráfico da função:
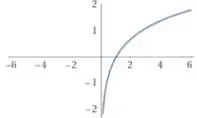
Só que na nossa função, o raio é o logaritmo natural do ângulo :
Vamos então discutir algumas características dessa função.
Passo 2
Sabemos que:
- A função envolve o logaritmo natural de , que cresce de forma lenta e gradual à medida que aumenta. Isso implica que o raio aumenta de forma gradativa à medida que nos afastamos da origem e criando uma curva que se expande indefinidamente em torno da origem.
- Como cresce muito lentamente, a função se comporta de maneira similar a uma espiral logarítmica, onde as voltas ficam cada vez mais espaçadas à medida que nos afastamos da origem.
- O intervalo cobre múltiplas voltas no plano polar, permitindo observar o comportamento completo da espiral.
- O raio aumenta logaritmicamente com , o que significa que a espiral se torna mais espaçada à medida que se afasta da origem.
- A origem é um ponto importante onde a espiral começa, além disso, a espiral não tem extremos definidos, pois continua a se expandir infinitamente com .
Passo 3
Vamos começar analisando a função de usando o intervalo dado,
O começa em e aumenta continuamente, isso significa que para nossa curva polar, aumenta conforme aumenta, o que significa que segue uma forma espiral similar aos gráficos e .
Passo 4
Analise dos demais gráficos.
O gráfico parece crescer com um passo constante enquanto o gráfico começa a crescer mais devagar próximo do final do intervalo, baseado no fato de que as linhas estão mais próximas.
começa a crescer a uma taxa mais lenta. Portanto, baseada nessa informação, podemos combinar com o gráfico .
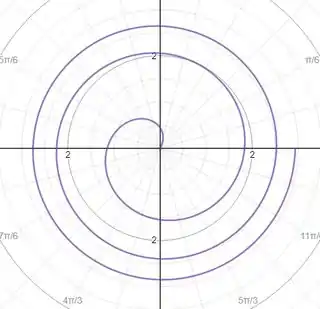
Resposta
O Gráfico correspondente é o .