Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 54d
Combine as equações polares com os gráficos com os gráficos . Dê os motivos das suas escolhas. (Não use ferramentas gráficas.)
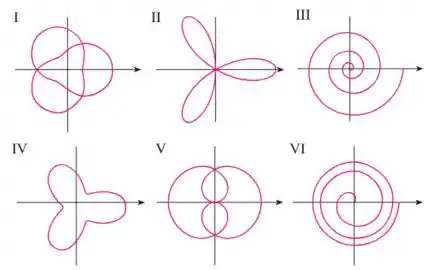
Passo 1
Faala ae, beleza?? Bom... o enunciado nos deu a seguinte equação polar:
E queremos desenhar o seu gráfico. Para isso, o enunciado já nos deu e disse que é um desses:
A nossa função aqui é descobrir qual dos gráficos representam a nossa equação polar!!
Para respondermos isso, vai partir do que a gente conhece da nossa equação.
Nesse caso, vamos começar analisar o que o cosseno nos tem a dizer e aí a gente vai implementando os outros termos da função e analisando com o comportamento.
Com essas análises, a gente vai descartando os gráficos que não fazem sentido com o que estamos pensando.
Agora bora lá!! 😉
Passo 2
Bom... vamos relembrar a nossa equação:
Olha... a gente pode começar analisando o cosseno!!
A gente sabe que o cosseno é uma onda periódica que a amplitude varia entre e da seguinte forma:
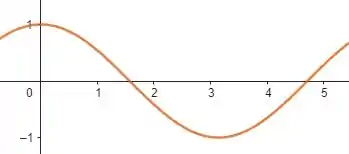
Ao multiplicarmos o seu ângulo por , estamos aumentando as oscilações em vezes, ou seja:
E, somando na função, estamos fazendo com que seu pico seja e seu vale seja , veja:
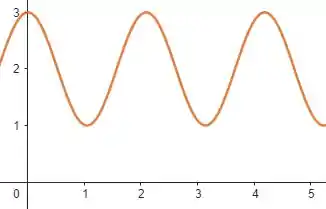
Tá... mas o que a gente pode concluir daqui sobre a impressão dessa plotagem em um gráfico polar???
Como podemos ver, não cresce conforme aumenta, o que já nos leva a excluir os dois gráficos espirais.
Além disso, não assume valores menores que , o que nos deixa com duas opções: e .
Passo 3
Pensa aqui comigo, o assume valor quando . O ângulo que isso acontece é:
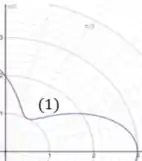
Logo, a gente espera que a primeira curva (1) varie de até em menos da um quadrante completo. Já que o quadrante tem radianos e a atinge em . Beleza?
Além disso, vemos pelo gráfico do passo , que quando o vai de até , podemos ver que a varia de até .
Opa, isso nos diz que ao terminar o primeiro quadrante, temos que estar em . Sempre no sentido anti-horário, ok??
Dessa forma, temos a curva (1), na figura abaixo.
Passo 4
De até um pouco antes de temos que chega a de novo.
Como é na metade do segundo quadrante, esperamos que aconteça bem próximo à metade do segundo quadrante, montando metade da curva .
Depois desse valor até , nosso variou de até de novo, logo, terminamos a curva (2) em , que é no final do segundo quadrante:
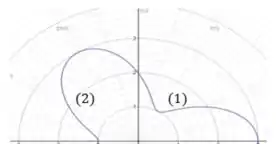
Continuando, de até um pouco depois de (ou seja, um pouco depois da metade do terceiro quadrante) temos que variou de até de novo.
E, daí até (final do terceiro quadrante), chegou a , construindo nossa curva (3).
Vamos continuar com esse raciocínio para chegar na curva (4).
Pois vemos que deve bater antes da metade do quarto quadrante e terminar esse último quadrante () em .
Com isso, chegamos nessa figura aqui:
Beleza?? Logo, nossa resposta é a .
Resposta
O Gráfico correspondente é o .