Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 23
Combine o gráfico das funções mostradas em (a) a (f) com os de suas derivadas em (A) a (F).
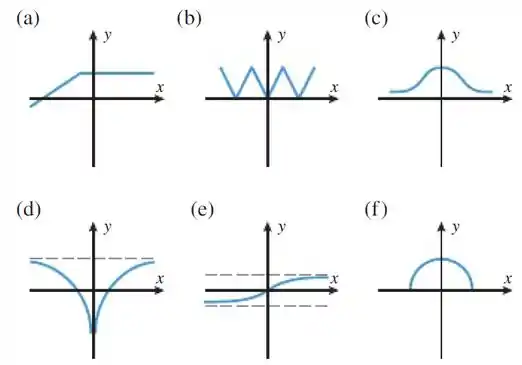
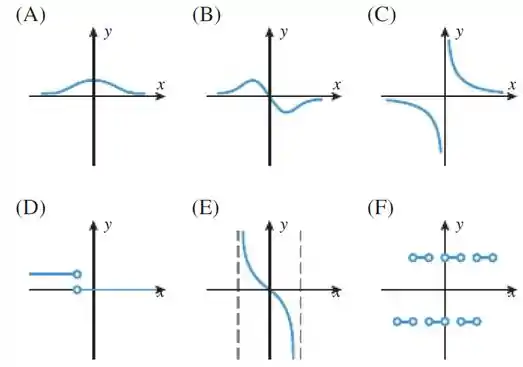
Passo 1
Vamos analisar cada gráfico à procura do gráfico de sua derivada, começando pelo gráfico da letra a):
A função do gráfico a) está aumentando constantemente no lado esquerdo e depois fica constante no lado direito, então temos que a derivada é constante no lado esquerdo e é igual a zero no lado direito, assim o gráfico da derivada associado é o da letra D).
Passo 2
A função do gráfico b) está constantemente diminuindo e aumentando, então temos que a derivada deve ser constante negativa e constante positiva, e assim indo, assim o gráfico da derivada associado é o da letra B).
Passo 3
A função do gráfico c) está aumentando no lado esquerdo e diminuindo no lado direito, então temos que a derivada deve ser positiva no lado esquerdo e negativa no lado direito, assim o gráfico da derivada associado é o da letra B).
Passo 4
A função do gráfico d) está diminuindo no lado esquerdo e aumentando no lado direito, então temos que a derivada deve ser negativa no lado esquerdo e positiva no lado direito, assim o gráfico da derivada associado é o da letra C).
Passo 5
A função do gráfico e) está aumentando em todos os lugares, temos então que a derivada deve ser positiva em todos os lugares, assim o gráfico da derivada associado é o da letra A).
Passo 6
E por último, a função do gráfico F) é definida em um intervalo limite, então temos que a derivada também deve ser definida no mesmo intervalo limitado, assim o gráfico da derivada associado é o da letra E).
Resposta
(a) (D)
(b) (F)
(c) (B)
(d) (C)
(e) (A)
(f) (E)