Faça um esboço cuidadoso de e abaixo dele esboce o gráfico de como foi feito nos Exercícios . Você pode sugerir uma fórmula para a partir de seu gráfico?
Passo 1
A primeira coisa que temos que fazer aqui é desenhar o gráfico da nossa função exponencial . Ele é desse jeito aqui:
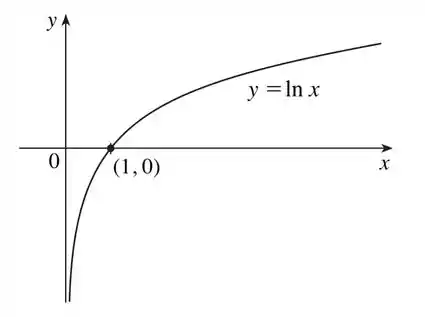
Passo 2
Nosso próximo passo vai ser desenhar algumas retas tangentes no gráfico da função logarítmica para ter uma ideia do que esperar do gráfico de sua derivada. A próxima imagem mostra algumas dessas retas, saca só:
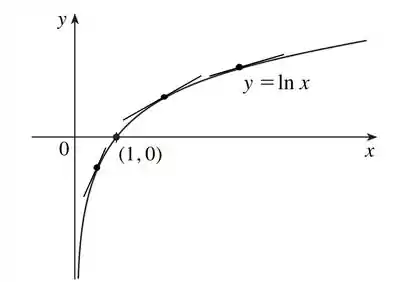
Já podemos tirar algumas conclusões de como vai se comportar – a primeira é que, pelo visto, as retas tangentes à sempre vão ser crescentes, então a função vai ser sempre positiva, entendeu?
Outra conclusão é que, a medida que caminhamos no gráfico para a direita no eixo , essas retas tangentes vão ficando menos inclinadas, ou seja, o valor da derivada vai diminuindo. Por outro lado, se a for um número beeem pequenininho, vai ser muito alto, aumentando mais e mais a medida que tende à zero.
Passo 3
Já podemos esboçar o gráfico de com base no que n que descobrimos! Vamos pensar: Quando cresce muito, decresce muito. Quando é bem pequeno, será bem grande. Pelo visto, e são grandezas inversamente proporcionais, logo, podemos arriscar esse gráfico aqui como esboço:
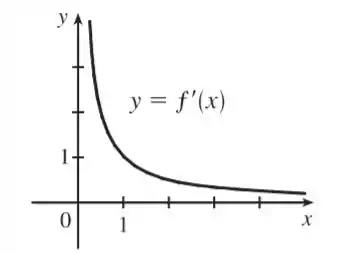
Como diminui quando aumenta, podems sugerir que a função derivada é a função recíproca, ou seja, .
Resposta
O esboço de vai ficar dessa forma:
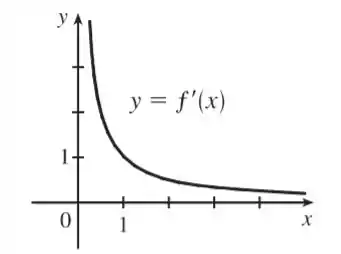
E a expressão que podemos sugerir para essa derivada é .