Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 8.4 - Ex. 11

Uma companhia modelou a curva de demanda para seus produtos (em dólares) pela equação:

Use um gráfico para estimar os níveis de vendas quando o preço de venda é de . Então encontre (aproximadamente) o excedente do consumidor para os níveis de vendas.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos plotar a curva dada no enunciado e avaliar o ponto em que ela vale .

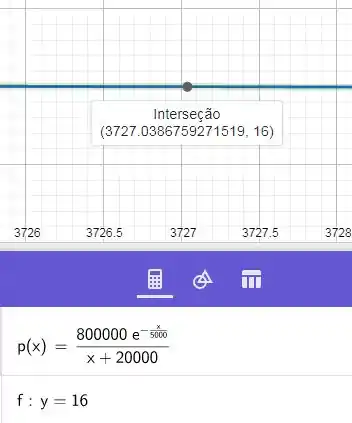
Podemos ver que o nível de vendas é de cerca de , quando o preço de venda é de . Agora, temos que , , e o excedente do consumidor para o nível de vendas de é:

Passo 2

Vamos trabalhar com letras pra não confundirmos os números constantes. Seja , , e . O excedente será:

Para resolver as integrais joguei em uma calculadora e obtive os seguintes valores:

O valor aproximado do excedente é de .

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A função custo marginal é dada por C ' = 3 x 2 + 8 x + 4 e o custo geral é $ 6 . Ache a função custo geral.

Um colecionador de arte comprou uma pintura por $1000 de uma artista cujos trabalhos aumentam de valor em relação ao tempo, de acordo com a fórmula d V d t = 5 t 3 2 + 10 t + 50 , onde V é o valor est

Uma equação da reta tangente à curva no ponto (1,3) é y = - 2 . Se em qualquer ponto x , y da curva d 3 y d x 3 = 2 , ache a equação da curva.

O volume de água num tanque é V m 3 quando a profundidade da água é h m. Se a taxa de variação V em relação a h for π 4 h 2 + 12 h + 9 , ache o volume de água no tanque quando a profundidade for de 3m

Uma equação da reta tangente à curva no ponto (1,1) é y = 2 - x . Se em qualquer ponto x , y da curva d 2 y d x 2 = 1 - x 2 , ache a equação da curva.