Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.1 - Ex. 54
Uma companhia de táxi cobra pela primeira milha (ou fração dela) e centavos a cada décimo de milha adicional (ou fração). Expresse o custo de uma corrida como uma função da distância percorrida (em milhas) para e esboce o gráfico.
Passo 1
E aí galera! Aqui nessa questão, queremos expressar o custo cobrado pela companhia de táxi sob a forma de função e esboçar o gráfico da mesma.
Para isso, devemos lembrar os dados fornecidos pelo enunciado:
- Até uma milha o valor da viagem fica sendo , ou seja, nosso custo será no intervalo
- Acima de 1 milha para cada de milha são cobrados centavos a mais, assim, devemos quebrar nosso intervalor de até chegarmos em .
Essa função não vai ser contínua. Ela vai ser dividida em parte e se parecer com uma escadinha, porque a variação de preço só acontece quando a cada milhas (depois da primeira milha).
Vamos ver intervalo por intervalo.
Passo 2
Se a primeira milha, seja inteira ou uma parte dela, custa , então a função começa assim:
Agora, até milhas, vamos adicionar apenas centavos a mais:
Até milhas, vamos adicionar apenas centavos a mais, ficando com :
E com essa mesma lógica, completamos todos os intervalos:
Passo 3
Agora pra plotar esse gráfico, precisamos entender a forma dele. Como eu disse no passo 1, ele vai ter uma forma de escadinha. Isso porque ele é sempre definido por constantes, mas de valores diferentes pra cada intervalo. Então é só a gente montar a altura dos degraus, de acordo com o valor da função:
Com a ajuda de um software matemático vamos obter:
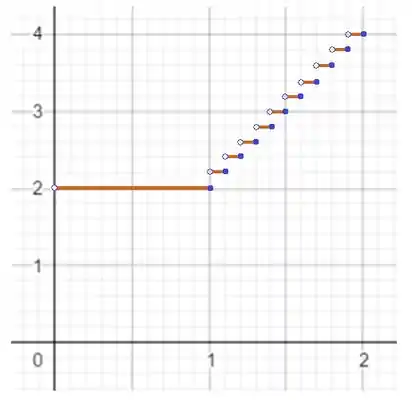
Resposta
