Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.1 - Ex. 40

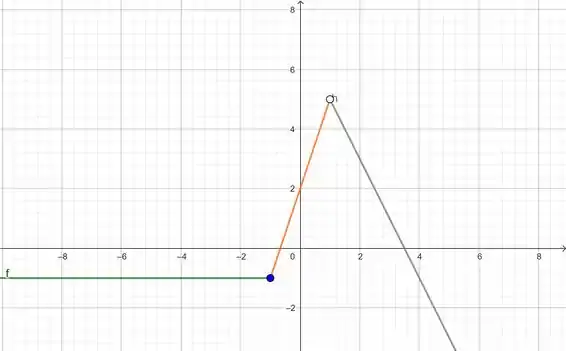
Encontre o domínio e esboce o gráfico da função

Passo 1

Olá, meu querido estudante. Estarei aqui te ajudando a resolver mais uma atividade.

A questão nos pede para encontrar o domínio da função, ou seja, quais valores de nós temos na função de tal forma que ela exista e, além disso, pede para que plotemos o gráfico dessa função definida em segmentos.

Para plotarmos o gráfico iremos utilizar o GeoGebra, deveremos ficar atentos principalmente aos pontos em que ocorrem as mudanças de equações.

Passo 2

Ao se analisar o domínio da função, devemos observar quais restrições nós temos. Nessa função, não existem restrições, qualquer valor de pode ser utilizado, sendo assim:

Em relação ao gráfico, estarei utilizando o GeoGebra para plotar:

Primeiro, vamos plotar para

Temos uma constante aqui: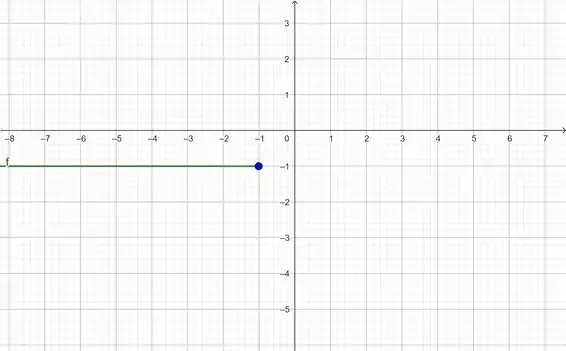

Como o ponto pertence a esse intervalo, colocamos o ponto fechado.

Agora vamos adicionar a equação

Veja que para:

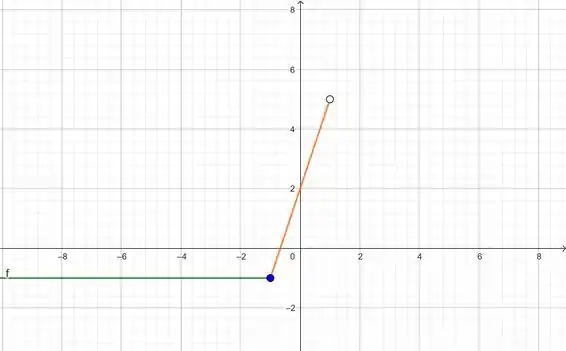
Como não pertence a essa equação, então deixamos o ponto aberto.

Última equação a ser adicionada é a:

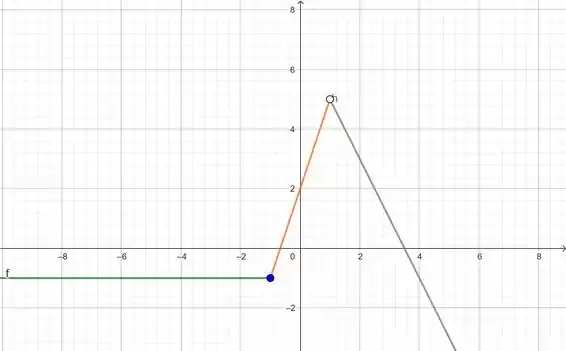
E aqui terminamos nossa resolução!!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um avião voa a uma velocidade de 350k m / h , a uma altitude de 1k m e passa diretamente sobre uma estação de radar no instante t = 0 . Expresse a distância horizontal de voo d (em quilômetros) como u

Se f x = x + 4 e h x = 4 x - 1 , encontre uma função g tal que g ∘ f = h .

Sejam f x = 3 x - 2 e g x = x . Em cada parte, dê a fórmula para a função e o correspondente domínio.(a) f + g (b) f - g (c) f g (d) f / g

Sejam f x = 2 - x 2 e g x = x . Em cada parte, dê a fórmula para a composição e o correspondente domínio.(a) f ∘ g (b) g ∘ f

Sejam f (x) = sqrt(x) e g (x) = x^3 + 1 . Determine:(a)f ( g (2) ) (b)g ( f (4) ) (c) f ( f (16) ) (d)g ( g (0) ) (e) f ( 2 + h ) (f) g ( 3 + h )