Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.1 - Ex. 58
Uma companhia de táxi cobra pelo primeiro quilômetro (ou parte de quilômetro) e centavos a cada décimo de quilômetro adicional (ou parte disso). Expresse o custo (em dólares) de uma corrida como uma função da distância percorrida (em quilômetros) para e esboce o gráfico desta função.
Passo 1
Essa questão aqui é um pouquinho traiçoeira, mas não te preocupa não que vamos dar um jeito nela! Olha só:
Pelo enunciado, quando , ou seja, no primeioro quilômetro, teremos que . Até aí ok né? Temos que ter cuidado principalmente com a próxima parte.
A cada décimo de quilômetro ou fração de décimo de quilômetro, adicionamos centavos no valor. Por exemplo: quando , vamos ter . Sacou? Esses acréscimo de centavos vai ser válido durante esse pequeno intervalo. Isso vai acontecer mais vezes na nossa função: vamos ter pequenos intervalos onde devemos ter um acréscimo de centavos. A expressão de vai ficar assim:
Pronto! Ficou escrito de uma forma grande e meio estranha, mas é isso mesmo: essa função é definida por várias sentenças.
Passo 2
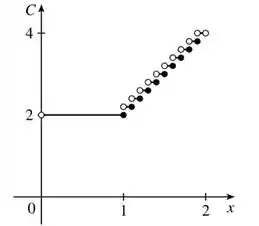
Para desenhar o gráfico, temos que desenhar o que acontece para cada intervalo de . No final das contas, nosso gráfico ficará assim:
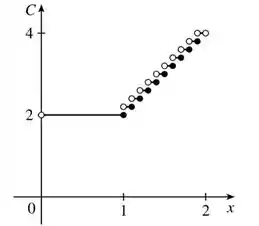
No gráfico, temos várias retas bem pequenas, paralelas ao eixo horizontal, cada uma representando uma sentença da nossa função. É importante ressaltar que essas bolinhas brancas no inicio da cada reta significam que o ponto não ta incluso nela, enquanto a bolinha preta significa que ta incluso, beleza?
É isso, acabou a nossa questão!
Resposta
