Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.1 - Ex. 49
Encontre o domínio e esboce o gráfico da função.
43)
Passo 1
E aí! tudo certinho? 👀
Nesse problema foi dada a função
E nosso objetivo é determinar o domínio e esboçar o gráfico da função.
Parece complicado? 🤔
Muito bem galera, o domínio são os valores que o pode assumir.
Já para esboçar o gráfico dessa função, podemos analisar como a função se comporta em cada uma de suas partes...
Veja só! 😇
Passo 2
De acordo com o enunciado, temos todos os valores de . Sendo assim pode assumir qualquer valor, ou seja
Agora vamos desenhar o gráfico desta função. Lembrando que:
E:
Dessa forma, para plotamos o gráfico da reta e para plotamos o gráfico da parábola , resultando em
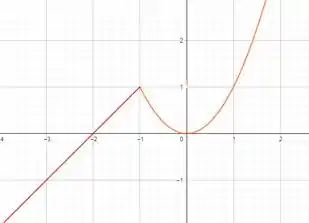
E terminamos! Entendeu tudo? Responde Aí! 😉
Resposta
Exercícios de Livros Relacionados
Se f x = x + 5 e g x = x 2 - 3 , resolva: f g 0 g f 0 f g x g f x f f - 5 g g 2 f f x g g x
Se f x = x - 1 e g x = 1 / ( x + 1 ) , resolva: f g 1 / 2 g f 1 / 2 f g x g f x f f 2 g g 2 f f x g g x
Determine os domínios e as imagens de f , g , f / g , g / f f x = 1 g x = 1 + x
Se f x = x + 5 e g x = x 2 - 3 , resolva: f g 0 g f 0 f g x g f x f f - 5 g g 2 f f x g g x
Se f x = x + 5 e g x = x 2 - 3 , resolva: f g 0 g f 0 f g x g f x f f - 5 g g 2 f f x g g x