Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.5 - Ex. 27
Compare as funções e traçando e em várias janelas retangulares. Quando o gráfico de ultrapassa o de ?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente comparar as funções e através do esboço de seus gráficos em várias janelas retangulares e dizer quando o gráfico da função ultrapassa o da função .
Pra isso, temos que ter em mente que estamos trabalhando com uma função potência () e uma função exponencial (), que são duas coisas diferentes, tá? Porque na função potência, a variável é a base e na exponencial, a variável é o expoente.
No caso da nossa função exponencial, temos como base o número , que é aproximadamente . Essa função é chamada de exponencial natural e ela vai sempre ter uma inclinação igual a e cortar o eixo no ponto .
No caso da nossa função potência, temos um polinômil de grau , que lembra o gráfico de uma parábola mais achatada na origem.
Com essas informações e com o auxílio de um software, conseguimos traçar o gráfico das duas e comparar o comportamento gráfico delas, verificando o ponto onde elas se encontram e onde uma ultrapassa a outra.
Vamos lá!
Passo 2
Vamos começar esboçando o gráfico de e em uma janela retangular por :
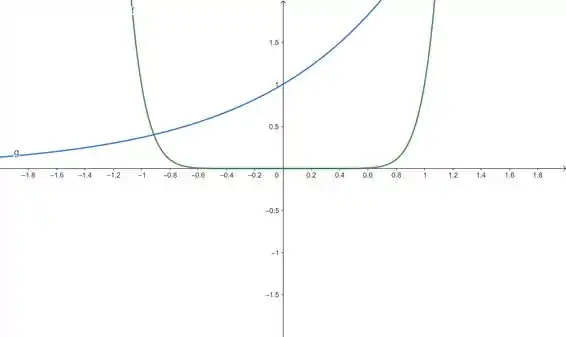
Observe que em verde temos o gráfico de e em azul o de . Repare que não dá pra dizer em que momento as curvas se interceptam ainda. Então, vamos ampliar nossa janela de visualização no software.
Passo 3
Utilizando agora uma janela retangular por , onde varia de a e também, vamos ter o gráfico:
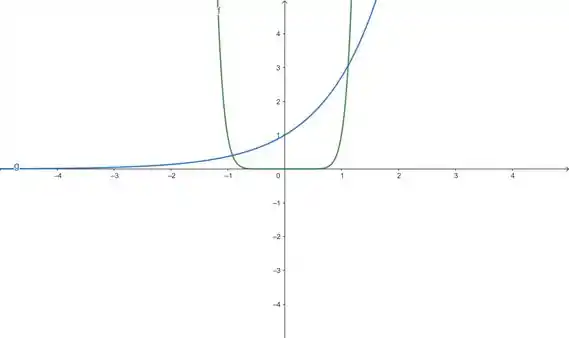
Agora nós já conseguimos ver os pontos de encontro entre as duas curvas. Observe que para , o gráfico de já fica acima do gráfico de .
Vamos dar um zoom para ver melhor:
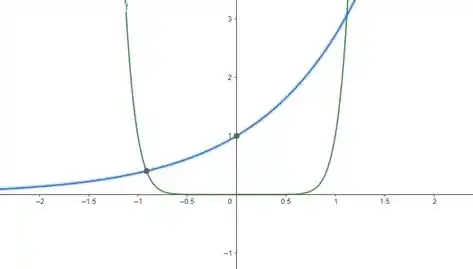
Observe que a curva em azul, vem crescendo muito próxima do eixo até que encontra a curva (em verde) e começa a crescer muito mais rapidamente que a função potência. Então, nós podemos dizer que a função exponencial ultrapassa para valores maiores do que , aproximadamente.
Valeu, galera! Até a próxima! 😉