Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.5 - Ex. 2
- Como é definido o número ?
- Qual o valor aproximado de ?
- Qual a função exponencial natural?
Passo 1
Opa, bora lá!
Essa questão é mais teórica, então ela é um pouco mais direta, né?
Na letra a, mostramos como o número é definido.
Na letra b, dizemos o valor aproximado de .
Na letra , vamos falar qual é a função exponencial natural.
Passo 2
Na letra (a) queremos a definição de , o número neperiano.
A ideia é a seguinte: queremos um número que, quando colocado como base de uma função exponencial , forma um gráfico de forma que a reta tangente no ponto tem inclinação igual a . Isso quer dizer que procuramos uma função em que a tangente vale 1, como na figura:
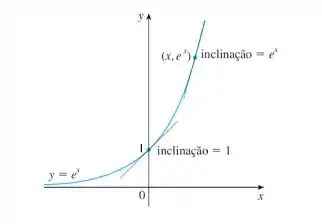
Esse número é o !
Passo 3
Para a letra (b), temos que o valor aproximado de é , esse já é um valor tabelado e beeeem conhecido, então a gente só grava ele (ou só grava que é aproximadamente que já vai ser suficiente pra quase todas as questões).
Passo 4
Na letra (c), temos que a função exponencial natural é aquele em que é a base da potência, assim como queríamos no passo 1:
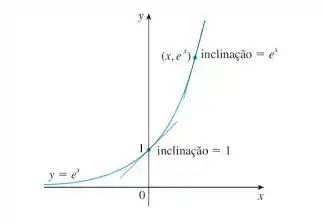
Prontinho!
Resposta
(a) é a base da função exponencial cujo gráfico tem tangente de inclinação em .
(b)
(c) A função exponencial natural é