Trace o gráfico de diversos membros da família de funções
em que . Como o gráfico muda conforme varia? Como ele muda conforme varia?
Passo 1
A questão fornece uma família de funções dada por
Devemos plotar várias curvas para diferentes valores de e . Primeiro, vamos fixar e ver como a curva muda quando varia:
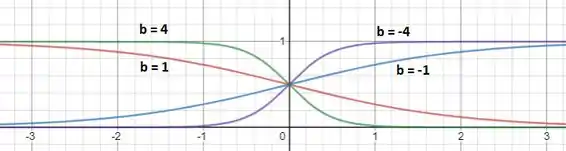
Vemos que todas as curvas passam pelo ponto e que todas são simétricas com relação a ele. Vemos também que quando invertemos o sinal de a simetria também é invertida!
Por fim, quando aumenta em módulo, a curva atinge sua saturação mais rapidamente!
Passo 2
Agora vamos fixar e ver como a função muda conforme varia:
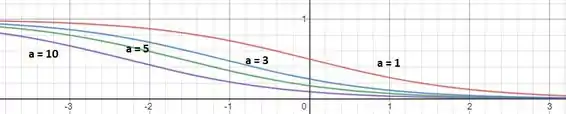
Vemos que, conforme cresce, a curva vai se deslocando para trás.
Resposta
Esboço de gráfico.