Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.9 - Ex. 21
Use o método de Newton para encontrar todas as raízes da equação corretas até a sexta casa decimal.
Passo 1
Fala aí! tudo certinho?
Nesse problema temos que encontrar as raízes da equação:
Utilizando o método de Newton com precisão de 6 casas decimais.
Tem ideia de como fazemos isso?
Primeiro vamos transformar nossa equação em uma função lavando tudo para um lado da igualdade.
O método de Newton é dado pela formulinha:
Onde repetimos os cálculos em ciclos até uma precisão de, no caso, casas decimais. Ou seja, quando até a casa.
Show? Bora começar!
Passo 2
Vamos começar calculando a derivada de para montar nossa formulinha do método de Newton.
Pela regra da potência e pelo teorema fundamental do calculo, temos:
Então a fórmula fica:
Agora basta escolher uma aproximação inicial adequada, e então aplicar a fórmula até os resultados não diferirem na sexta casa decimal.
Para escolher o valor inicial olhamos um esboço das funções e .
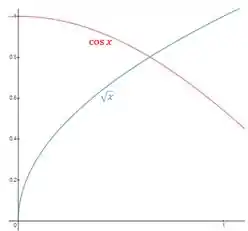
Há uma raíz entre e , então é uma boa aproximação inicial.
Bora começar!
Passo 3
Então calculamos as próximas aproximações:
Para , temos:
Continuando para ...
Calculando :
ainda não se repetiu, então vamos calcular
Agora calculando ...
Calculando :
...
E :
E finalmente!! , então a equação possui uma raiz próximo de .
É isso! O que achou? Responde Aí!