Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.1 - Ex. 11
(i) Complete a tabela e dê um palpite sobre o limite indicado
(ii) Confirme suas conclusões sobre o limite desenhando o gráfico da função sobre um intervalo adequado
;
Passo 1
(i) Não tem mistério: aqui é só jogar os valores de da tabela na função e calcular . Agora, é claro que fazer isso na mão fica complicado. Sugiro que você use uma calculadora gráfica ou mesmo o Excel pra isso.
Jogando esses valores no Excel ou na calculadora, vamos ter então, respectivamente para :
Passo 2
(ii) Temos pra essa função o gráfico:
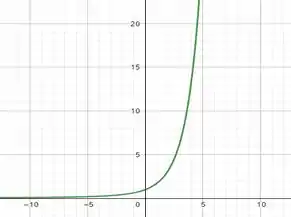
Precisamos, ainda, calcular o limite pra confirmar o que vemos no gráfico. Pra isso, vamos começar com uma mudança de variável pra nos ajudar no cálculo. Consideraremos que:
Assim, por consequência:
Assim, quando , , já que . Reescrevemos o limite assim:
Mas, no que isso nos ajuda? Vamos entender! Fazemos uma pequena manipulação, dividindo numerador e denominador por , assim:
Pela propriedade do expoente do logaritmando (termo do logaritmo), podemos escrever isso assim:
Passo 3
Como logaritmo é uma função contínua, o limite da função logaritmo equivale ao logaritmo do limite da função. Conseguiu entender, ou muito confuso? Escrevendo isso matematicamente você vai entender:
De conhecimentos prévios de Cálculo, você já deve ter ouvido falar (caso não, tente dar uma pesquisada rápida!) nos limites fundamentais. Um deles é o que acabou de aparecer no denominador, e tem seu vaor bem definido:
Isso resolve nosso problema, e podemos assim calcular o limite muito facilmente. Temos:
Olhando no gráfico, e pelos valores da função nos pontox próximos de 0, confirmamos que, de fato, quando tende a 0, a função tende a 1.
Resposta
Ei, a resposta está no passo a passo :)