Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.3 - Ex. 13
Calcule o limite, se existir.
13)
Passo 1
Bom galera, pra começar, o limite sempre existe se:
Pode acontecer do resultado do limite ser ou dele simplesmente ser incalculável. Nesses dois casos, dizemos que o limite não existe. Será que aqui a gente acha um número qualquer?
Passo 2
Bom galera, para começar vamos adaptar um pouquinho! Usando a propriedade :
Usando as propriedades e :
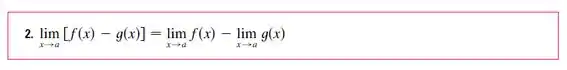
Usando a de número e :
Agora vamos aplicar a última, número :
Passo 3
Enfim, achamos:
Na prática, não dá pra dividir nada por zero né? Então dizemos que esse limite não existe. O que acontece é que quando chega bem perto de , a função:
Vai chegar bem perto de . Duvida? Da uma olhada no gráfico dessa função:
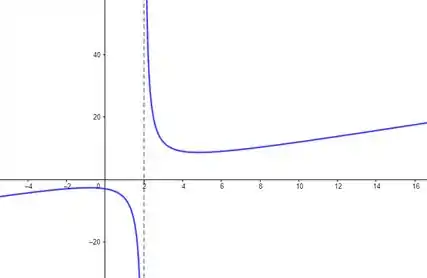
Então é isso galera, o limite não existe!
Resposta
Exercícios de Livros Relacionados
Expresse as somas em formas fechadas.sum_(k = 1)^n ((5)/(n) - (2 k)/(n))
Expresse as somas em formas fechadas.sum_(k = 1)^(n - 1) (k^2)/(n)
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.Cada aproximação pela extremidade direita da área sob o gráfico dey = x 2 acima de um intervalo [ a , b ] será uma superestim
Para uma função f que é contínua em [ a , b ] , a Definição 5.4 . 5 diz que a área líquida com sinal A entre f ( x ) e o intervalo [ a , b ] é: A =lim n → ∞ ∑ k = 1 n f x k * Δ x Dê interpretação ge
Use a Definição 5.4.3 tomando como a extremidade direita de cada subintervalo para encontrar a área sob a curva y = f ( x ) acima do intervalo especificado. f x = x 3 ; 2,6