Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 66
Por comportamento final de uma função queremos indicar uma descrição do que acontece com seus valores quando e quando .
- Descreva e compare o comportamento final das funções
- Dizemos que duas funções têm o mesmo comportamento final se sua razão tende a quando . Mostre que e têm o mesmo comportamento final.
e
por meio do gráfico de ambas, nas janelas retangulares por e por
Passo 1
Olá, meu querido amigo. Vamos resolver mais uma atividade hoje, e eu estarei aqui para te ajudar a resolver.
A gente aqui vai primeiramente descrever e comparar o comportamento das duas funções em diferentes janelas retangulares.
As janelas retangulares são delimitações utilizadas comumente por softwares gráficos, para gerar nossos gráficos. Como os eixos coordenados são infinitos, costumeiramente o que se faz é definir um intervalo de e para o qual se irá gerar e mostrar o usuário o gráfico da função.
Então em cada janela das mostradas, iremos visualizar uma porção diferente do mesmo gráfico. A partir então desses gráficos é que iremos comentar os seus comportamentos nas duas letras.
Passo 2
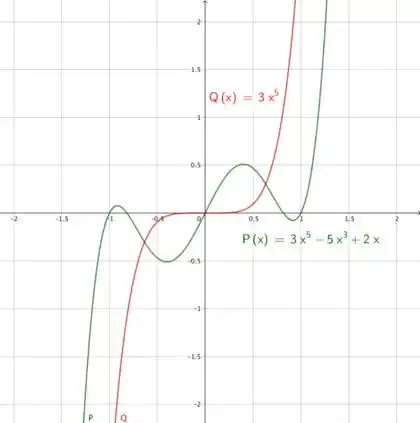
- Vamos começar analisando o comportamento das funções através de seus gráficos. Na primeira janela por , temos o seguinte:
- Para mostrar que o comportamento final é o mesmo, devemos verificar que:
Agora a análise na segunda janela por .
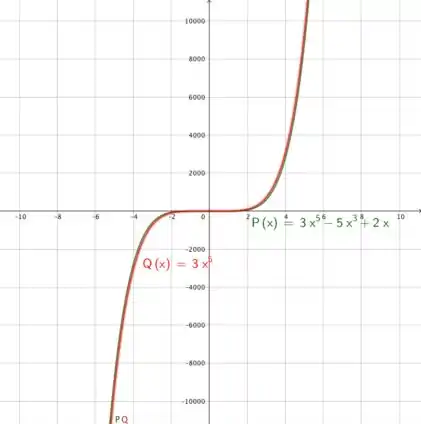
Pela análise dos gráficos, conseguimos intuir que:
e
Também conseguimos perceber que na segunda janela os gráficos são bem parecidos, isso também indica que o comportamento final dos gráficos será o mesmo. Na primeira janela isso não fica tão nítido, agora vamos provar que o comportamento final é o mesmo na letra b).
Passo 3
Vamos lá,
Aqui eu vou separar em 3 frações.
Simplificando então cada nas equações:
Calculando o limite de cada função individualmente e retirando as constantes do limite:
Calculando o limite:
Como o quociente tende para , concluímos que as funções têm o mesmo comportamento final. Já era de se esperar pela análise dos gráficos da questão a).
Resposta
- Ver o gráfico e o desenvolvimento.
- Como o quociente tende para , concluímos que as funções têm o mesmo comportamento final.