Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.1 - Ex. 27
Seja área sob o gráfico de uma função contínua crescente de até , e sejam e as aproximações para com subintervalos usando extremidades esquerdas e direitas, respectivamente.
- Como e estão relacionadas?
- Mostre que . Então desenhe um diagrama para ilustrar essa equação ,mostrando que retângulos representado podem ser reunidos num único retângulo cuja área é o lado direito da equação.
- Deduza que ,
Passo 1
O enunciado nos diz que: “Seja área sob o gráfico de uma função contínua crescente de até , e sejam e as aproximações para com subintervalos usando extremidades esquerdas e direitas, respectivamente.”
E a primeira coisa que ele nos pergunta é como e estão relacionadas!
Bora lá! Desde que é uma função crescente e sendo uma subestimativa (estimativa inferior ) e uma superestimativa (estimativa superior). Se liga na imagem pra ficar mais claro:
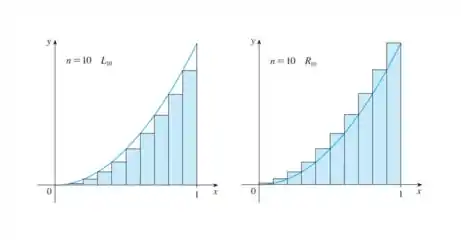
Então e estão relacionados pela desigualdades
Passo 2
Agora, na letra b o enunciado está pedindo pra a gente mostrar que:
E depois devemos desenhar um diagrama para ilustrar essa equação, mostrando que retângulos representado podem ser reunidos num único retângulo cuja área é o lado direito da equação.
Sendo:
E:
Subtraindo as igualdades:
Como .
Agora vamos para o diagrama:
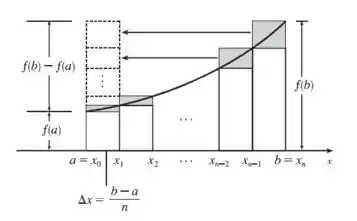
No diagrama é a soma das áreas dos retângulos sombreados. Deslizando os retângulos sombreados para a esquerda, de modo que eles se empilhem em cima do retângulo sombreado mais à esquerda, formamos um retângulo da altura e largura .
Passo 3
Pra acabar temos que então , isto é:
Resposta
Desenvolvimento acima