Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 12
Detemrine o volume do maior cone de revolução que pode ser inscrito em uma esfera de raio .
Passo 1
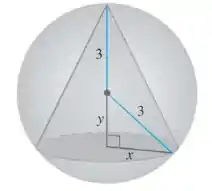
Vamos olhar a figura que ele deu no enunciado.
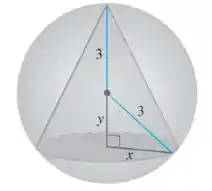
O volume desse cone vai ser área da base vezes a altura. Usando as variáveis que ele deu, vamos ter:
Mas olhando aquele triângulo retângulo de catetos e , e hipotenusa , vamso ter:
Isolando o
O volume vai ficar:
Aqui vai um detalhe bem doido rs
Vamos considerar que o varia de até . Poooooooooooo, medida negativa? Não é bem isso, escolhendo isso, estamos dizendo que na verdade é a distância do centro da esfera até a base do cone, mas distância vista como coodenada. Que assim pegarmos os cones como na figura ou um que tenha a base acima do centro.
Passo 2
Para acharmos o valor de mínimo ou máximo, temos que comparar o valor da função nos pontos críticos e nos extremos do intervalo.
Começando por achar os pontos críticos:
Fazendo isso igual a
Vamos ter:
Dividindo a equação por
Aplicando Bhaskaras, vamos ter:
Ou
Ambos servem. Bora.
Passo 3
Vamos achar o valor da função nos pontos críticos e extremos do intervalo:
Vamos ter:
O maior dos valores é quando
O maior valor é