Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 7

Uma área retangular em uma fazenda será cercada por um rio, e nos outros três lados sera usada uma cerca elétrica feita com apenas um fio. Com 800 m de fio à disposição, qual é a maior área que você pode cercar, e quais são as suas dimensões?

Passo 1

A nossa situação é a seguinte:

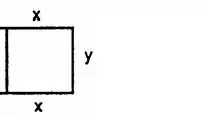
Onde aquela parte sem variável é o rio.

A área vai ser dada por

A = x y

Além disso, como vamos cerca apenas 3 lados, temos que a soma dos lados tem que ser igual ao comprimento do fio, ou seja,

2 x + y = 800

Assim,

y = 800 - 2 x

Substituindo na fórmula da área temo,

A = x 800 - 2 x

A = 800 x - 2 x 2

Agora vamos analisar o pontos crítico!

Passo 2

Para acharmos os pontos críticos, nós precisamos derivar e igualar a zero! Deste modo, ficamos com

A ' = 800 - 4 x

Fazendo isso igual a 0

800 - 4 x = 0

4 x = 800

x = 800 4

x = 200

Agora vamos calcular a área!

Passo 3

Substituindo o valor que encontramos para x na fórmula, temos

A = x 800 - 2 x

x = 200 → A = 200 800 - 2 200 = 200 800 - 400 = 200.400 = 80000

Entao o retângulo tem dimensões:

x = 200

y = 800 - 2 200 = 800 - 400 = 400

Resposta

Dimensão 200 × 400   m

Área máxima: 80000   m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma folha de papel retangular 8,5 × 11p o l . É colocada sobre uma superfície plana. Um dos vértices é colocado no lado maior oposto, como mostra a figura, e deixado lá enquanto a folha está aplanada.
28. Suponha que um peso deva ser mantido 10m abaixo de uma reta horizontal A B por um fio com a forma de Y . Se os pontos A e B estão a uma distância de 8m um do outro, qual o fio de menor comprimento
42. Se dois corredores em ângulo reto um com o outro têm larguras de 3 e 4,5m, qual o comprimento da maior viga que pode ser movida horizontalmente, passando por essa quina? Despreze a dimensão transv
Nos Exercícios 29 e 30, use a expressão competição perfeita. Quando uma empresa funciona em competição perfeita, há muitas firmas pequenas assim, nenhuma empresa afeta o preço ao elevar a sua produção
31. Sob um monopólio, que significa que há apenas um produtor de certa mercadoria, o preço e então a demanda podem ser controlados, regulando-se a quantidade da mercadoria produzida. Suponha que, sob