Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 54f
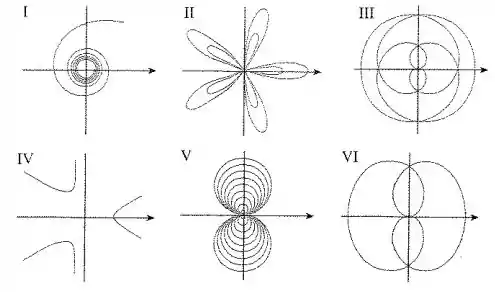
Conecte as curvas polares com seus respectivos gráficos I-VI.
Passo 1
A questão pede para ligarmos a curva dada em coordenadas polares a um dos gráficos disponíveis.
Neste caso, temos
Aqui não é uma função periódica de , a medida que cresce, nosso raio cresce também, então não temos uma periodicidade aqui, apenas um crescimento proporcional.
Passo 2
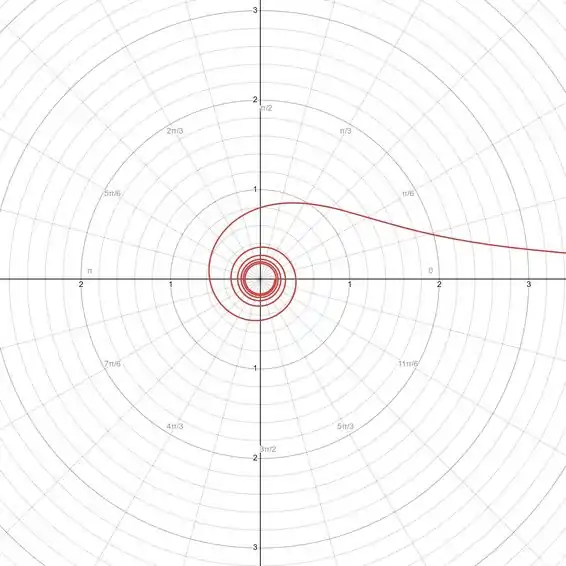
Conforme vai crescendo, vai diminuindo. Por outro lado, para muito próximo de , é muito grande...
Assim, conforme vai crescendo, vem lá de longe e se aproxima de , de modo que a curva vai expiralando para a origem. O gráfico I descreve isso perfeitamente!
Resposta
I
Exercícios de Livros Relacionados
Combine as equações polares com os gráficos com os gráficos I - V I . Dê os motivos das suas escolhas. (Não use ferramentas gráficas.) r = 2 + c o s 3 θ
Esboce a curva com a equação polar dada, esboçando primeiro o gráfico de r em função de θ nas coordenadas cartesianas. r = c o s θ 3
Esboce a curva com a equação polar dada, esboçando primeiro o gráfico de r em função de θ nas coordenadas cartesianas r = s e n θ 2
Plote o semicírculo traçado pela partícula no exercício 33(c).
a) Elimine o parâmetro para encontrar uma equação cartesiana da curva.b) Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = cosh t , y = s e n