Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 54c

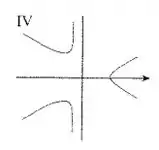
Conecte as curvas polares com seus respectivos gráficos I-VI.

r = sec ⁡ 3 θ

Passo 1

Opa, tudo tranquilo? A questão pede associarmos a seguinte curva em coordenadas polares

r = sec ⁡ 3 θ

Ou ainda

r = 1 cos ⁡ 3 θ

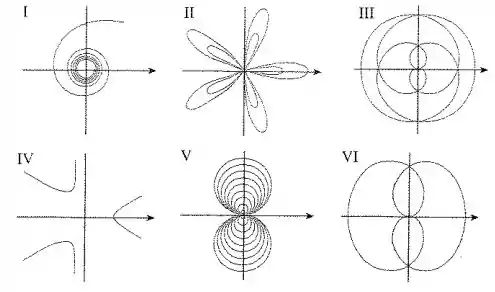
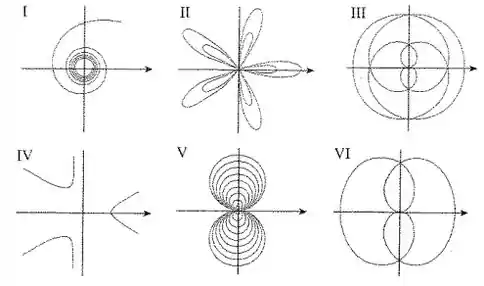
Ao gráfico adequado entre os seguintes

Dessa forma, nos vamos analisar a expressão da curva e tentar identificar características dela que nos ajudem a imaginar o formato do seu gráfico!

Passo 2

Para que essa função seja definida, o denominador não pode ser nulo! Como o cosseno está no denominador, devemos ter

cos ⁡ 3 θ ≠ 0

Mas ora, o cosseno é nulo para valores onde

π 2 + n π

Onde n é um número natural.

Dessa forma, podemos reescrever a desigualdade como

π 2 + n π ≠ 3 θ

Ou ainda

θ ≠ π 6 + n π 3

Desta forma, para alguns valores de θ , a curva não vai estar definida. A única curva que contempla essa possibilidade é a curva IV, já que as demais aparentam ser definidas para todos os valores de θ !

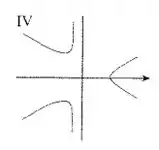
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a curva com a equação polar dada, esboçando primeiro o gráfico de r em função de θ nas coordenadas cartesianas. r 2 = c o s ⁡ ( 4 θ )
Esboce a curva com a equação polar dada, esboçando primeiro o gráfico de r em função de θ nas coordenadas cartesianas. r 2 θ = 1
Esboce a curva com a equação polar dada, esboçando primeiro o gráfico de r em função de θ nas coordenadas cartesianas r 2 θ = 1
Combine as equações polares com os gráficos com os gráficos I - V I . Dê os motivos das suas escolhas. (Não use ferramentas gráficas.) r = l n θ,1 ≤ θ ≤ 6 π ; r = θ 2 ,0 ≤ θ ≤ 8 π ; r = c o s 3 θ ; r
Combine as equações polares com os gráficos com os gráficos I - V I . Dê os motivos das suas escolhas. (Não use ferramentas gráficas.) r = l n θ,1 ≤ θ ≤ 6 π ; r = θ 2 ,0 ≤ θ ≤ 8 π ; r = c o s 3 θ ; r