Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 17
a) Elimine o parâmetro para encontrar uma equação cartesiana da curva.
b) Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
Oi, meu amigo. Vou te ajudar a resolver a atividade.
O problema fornece uma curva na forma parametrizada e pede para encontrarmos uma equação cartesiana que relacione e .
Neste caso, temos:
Para esse problema você lembrar que:
Que é a identidade trigonometria hiperbólica. Iremos utilizar essa relação para descobrirmos a equação cartesiana, isso é, uma relação entre e em uma mesma equação, e resolvermos essa atividade.
Após termos encontrado a equação cartesiana, iremos então prosseguir com o gráfico da função.
Para isso iremos nos atentar qual a figura gerada pela equação cartesiana, e iremos observar o que acontece com e quando aumentamos os valores de .
Criar um gráfico, caso você não saiba previamente o comportamento da função, é você encontrar os pontos de encontro entre os eixos, e também analisar o comportamento da função com diversos valores de .
Passo 2
Dada a nossa parametrização:
A gente vai jogar esses valores na identidade comentada no passo 1:
Assim, a equação cartesiana da curva é a hipérbole:
Mas cuidado, não podemos desenhar a hipérbole toda, pois:
E consequentemente:
Apenas um dos ramos da hipérbole deve ser desenhado! Então temos uma hipérbole que toca o eixo em:
Fazendo um esboço da curva...
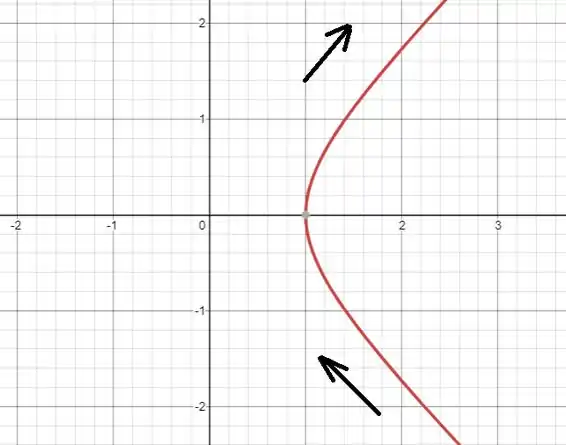
Conforme aumenta, cresce!