Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 54e
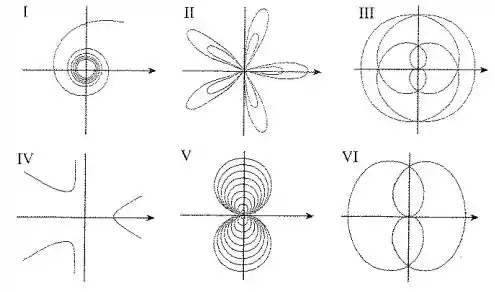
Conecte as curvas polares com seus respectivos gráficos I-VI.
Passo 1
A questão pede para ligarmos a curva dada em coordenadas polares a um dos gráficos disponíveis.
Neste caso, temos
E para encontrarmos a curva correspondente é importante aqui a gente analisar o comportamento da curva polar.
A periodicidade da curva é determinada por
E para a resolução dessa questão observar a periodicidade é de extrema importância.
Passo 2
Desta forma, entre e , a curva é divididade em partes com comportamento idêntico. Note que o gráfico apresenta cinco pétalas: ele é perfeito para descrever esse comportamento!
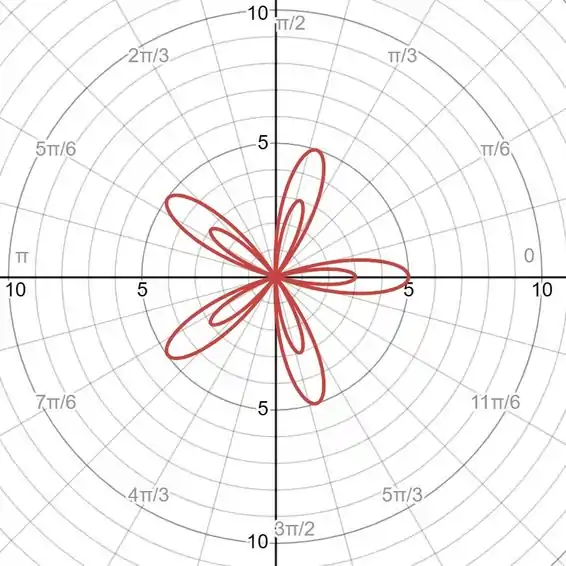
Resposta
II
Exercícios de Livros Relacionados
Descreve o movimento de uma partícula com posição ( x ,y ) quando t varia no intervalo dado. x = cos 2 t , y = cos t ,0 ≤ t ≤ 4 π
Encontre os pontos nas curvas dadas onde a reta tangente é horizontal ou vertical.61. r = 3 c o s θ
Encontre os pontos nas curvas dadas onde a reta tangente é horizontal ou vertical.63. r = 1 + c o s θ
Ligue as equações paramétricas aos gráfico de I-VI. x = s e n3 t , y = s e n4 t
Ligue as equações paramétricas aos gráfico de I-VI. x = t + s e n2 t , y = t + s e n3 t