Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 22
Descreve o movimento de uma partícula com posição ) quando varia no intervalo dado.
Passo 1
Para descrever o movimento de uma partícula com posição em função do parâmetro no intervalo , onde e , podemos analisar como x e 𝑦 variam com .
Relação entre 𝑥 e y:
A partir das equações dadas:
Podemos manipular a primeira equação para isolar . Sabemos que , Portanto:
Para determinar o sinal (), consideramos o intervalo . Sendo assim será sempre positivo neste intervalo. Sendo assim,
Passo 2
Para a segunda equação substituímos em :
A equação representa uma curva no plano cartesiano. É uma curva semelhante à metade superior de uma parábola aberta para cima, onde é a raiz quadrada de .
Passo 3
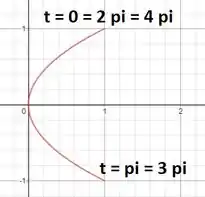
Que tal analisarmos o intervalo para construirmos o gráfico? Se liga!
Como varia de a , a partícula percorrerá a curva no intervalo em que varia de a (pois varia de a quando ).
Com isso, entendemos que ao longo do intervalo , a partícula descreve a curva representada a seguir pela equação no plano cartesiano.
