Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 28c
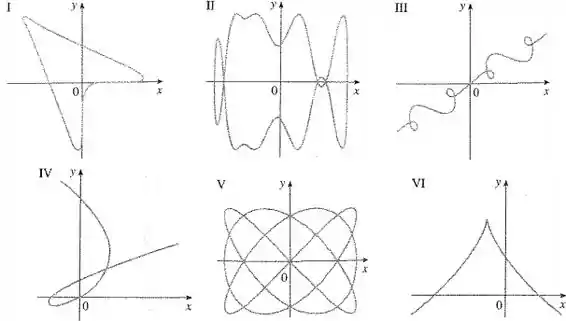
Ligue as equações paramétricas aos gráfico de I-VI.
Passo 1
Olá, meu querido amigo. Vou estar te ajudando a resolver essa atividade.
A questão fornece uma curva parametrizada e pede para identificarmos o seu gráfico.
Nesse caso, a gente tem a curva paramétrica:
Para resolvermos essa questão sem de fato plotarmos o gráfico da curva paramétrica, apenas analisando a equação, nós deveremos analisar pontos importantes da função.
Deveremos analisar interseção com os eixos, deveremos analisar o que ocorre quando , deveremos analisar periodicidade da nossa função. A estratégia aqui é analisar os pontos importantes de uma função e notar qual gráfico corresponde, ao fazer isso, por exclusão a gente consegue encontrar o nosso gráfico.
Passo 2
Aqui ambas as funções são periódicas. Desta forma, devemos esperar que a curva seja fechada!
Para achar as interseções com o eixo , fazemos :
Para .
Já para as interseções com o eixo , fazemos :
Para .
Assim, devemos ter mais interseções com o eixo do que com o eixo . Além disso, para , as curvas se encontram na origem. A única curva que reúne todas essas condições é a curva V.
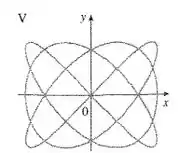
Resposta
V