Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 28d

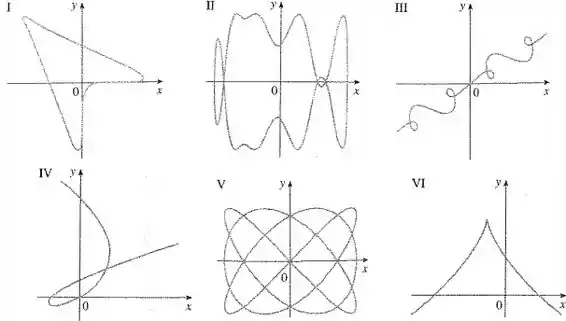
Ligue as equações paramétricas aos gráfico de I-VI.

x = t + s e n   2 t ,                     y = t + s e n   3 t

Passo 1

A questão fornece uma curva parametrizada e pede para identificarmos o seu gráfico.

Nesse caso,

x = t + s e n   2 t ,                     y = t + s e n   3 t

Para corresponder o gráfico com as funções, precisamos observar como as funções se comportam em alguns valores especiais.

Passo 2

Então vamos calcular o limite dessas funções para entendermos um pouco sobre o seu comportamento:

lim t → ∞ ⁡ t + sin ⁡ 2 t = ∞

E

lim t → ∞ ⁡ t + sin ⁡ 3 t = ∞

Vamos entender agora o comportamento para:

lim t → - ∞ ⁡ t + sin ⁡ 2 t = - ∞

E

lim t → - ∞ ⁡ t + sin ⁡ 3 t = - ∞

Observe que se não fosse as funções trigonométricas aparecendo, teríamos

x = t           e             y = t

Logo teríamos,

y = x

Como as funções trigonométricas só somam ou subtraem no máximo 1 , essa curva deve ser algo que oscile em torno da reta y = x .

Olha para o gráfico III e vê se ele não faz exatamente isso!

Resposta

III

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os vértices e os focos e as assíntotas da hipérbole e esboce o seu gráfico.21. y 2 - x 2 = 4
Use uma calculadora gráfica ou um computador para reproduzir a figura.
Use uma calculadora gráfica ou um computador para reproduzir a figura.
Faça um gráfico com vários membros das famílias de curvas x = s e nt + s e nn t , y = c o st + c o sn t , onde n é um número inteiro positivo. Quais as características que essas curvas têm em comum? O
Investigue a família de curvas dadas por r = 1 + c cos ⁡ θ , em que c é um número real. Como o formato muda conforme c varia?