Conforme a figura a seguir, um buraco cilíndrico é feito passando pelo centro de uma esfera. Mostre que o volume do sólido remanescente depende somente do comprimento do buraco e não do tamanho da esfera.
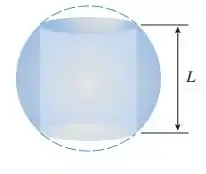
Passo 1
O que o enunciado está pedindo é para gente provar que o volume desse sólido só depende de .
A gente pode calcular esse volume por cascas cilíndricas, que tem essa carinha:
Isso para o volume de um sólido de rotação obtido quando a gente gira a área entre e o eixo , no intervalo , em torno de .
Vamos chamar o raio do cilindro de e o raio da esfera de . Colocando essas coisinhas numa figura, fica assim:
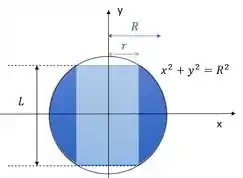
Vamos começar!
Passo 2
Podemos pensar que o nosso sólido é obtido pela rotação em torno de da área que está entre as retas e . E que também está dentro da circunferência .
Mas repara que essa região é simétrica em relação a . Então a área acima desse eixo e abaixo são iguais. Podemos dizer então que o nosso volume vai ser duas vezes o volume obtido pela rotação da área de cima.
Aplicando cascas cilíndricas, vemos que essa área está no intervalo e entre a função e o eixo . Por isso, a fórmulinha fica assim:
Mas nosso volume total é duas vezes esse volume, então temos que calcular:
Passo 3
Agora a gente calcula essa integral. Podemos usar uma substituição simples:
A integral fica:
Voltando para , já que :
Passo 4
Você deve estar pensando: ué, mas esse resultado depende de , então depende do tamanho da esfera. Nem aparece o ali.
Realmente, você tem razão. Mas relaxa. A gente pode usar nossa esperteza aqui. Olha essa figura:
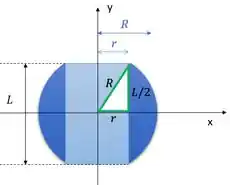
Tem um triângulo retângulo ali. Isso significa que a gente pode usar Pitágoras, nosso teorema amigo, para escrever:
Com isso, a gente pode reescrever o volume. Fica assim:
E assim, a gente prova que o volume só depende de . Arrasamos!
Resposta
Prova nos passos