Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.3 - Ex. 31

Use camadas cilíndricas para encontrar o volume do cone gerado quando o triângulo com vértices 0,0 ,   0 , r   e   ( h , 0 ) , sendo r > 0   e   h > 0 , gira em torno do eixo x .

Passo 1

Oiii tudo bem?

Essas sem valores específicos são enjoadinhas né?! Mas calma, vamos dar uma olhada em como seria a figura primeiro...

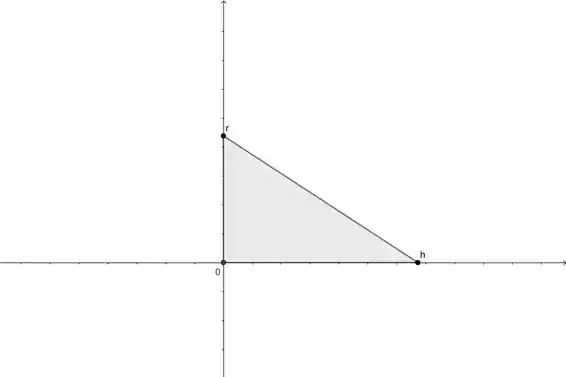
Lembrando que a gente quer rotacionar em torno do eixo x .

Passo 2

Bom, pra montar nossa integral com cascas cilíndricas, a gente vai precisar fazer aquela reta que vai de ( h , 0 ) até ( 0 , r ) , certo?

Então a gente tem que descobrir a função que passa por esses pontos.

A equação da reta é da forma: y = a x + b , sendo que b é onde a reta corta o eixo y (no caso b = r )   e a a gente pode achar substituindo um ponto na equação

Vamos substituir o ponto ( h , 0 ) :

0 = a h + r

a h = - r

a =   - r h

A equação da reta então é:

y =   - r h x + r

Só que a gente precisa da função em y , então:

x = h r r - y

É a que a gente vai usar.

Passo 3

Tendo as funções, vamos montar nossa integral para encontrar o volume do cone pedido...

A gente vai usar cascas cilíndricas, que é da forma:

V = ∫ a b 2 π y f y d y

Trazendo pro nosso caso fica:

V = ∫ 0 r 2 π y h r r - y d y

Resolvendo agora:

2 π ∫ 0 r y h - h r y d y

2 π ∫ 0 r y h - h r y 2   d y

2 π h ∫ 0 r y - 1 r y 2 d y

2 π h y 2 2 - 1 r y 3 3 0 r

2 π h r 2 2 - 1 r r 3 3

= 2 π h r 2 2 - r 2 3

= 2 π h r 2 6

= 2 π h r 2 6

V = π h r 2 3

Prontinho! Volume calculado😉

Resposta

V = π h r 2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo y . y = cos ⁡ x 2 , x = 0 , x = 1 2 π , y = 0
Sejam R 1 e R 2 regiões com a forma mostrada abaixo. Use camadas cilíndricas para encontrar o volume do sólido que resulta quando ( a ) a região R 1 gira em torno do eixo y . ( b ) a região R 2 gira e
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo y . y = e x 2 , x = 1 , x = 3 , y = 0
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo y . y = 1 / x , y = 0 , x = 1 , x = 3
Use camadas cilíndricas para encontrar o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.