Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.Revisão - Ex. 56

Seja F x = ∫ 0 x t 2 - 3 t 4 + 7 d x .

(a) Encontre os intervalos nos quais F é crescente e aqueles nos quais é decrescente.

(b) Encontre os intervalos abertos nos quais F é côncava para cima e o nos quais é côncava para baixo.

(c) Encontre os valores de x , se houver, nos quais a função F tem extremos absolutos.

(d) Use um CAS para fazer o gráfico de F e confirme que os resultados de (a), (b) e (c) estão de acordo com o gráfico.

Passo 1

(a) Para responder essa precisamos analisar o sinal da derivada de F . Podemos calcular essa derivada pela parte 2 do Teorema Fundamental do Cálculo:

d d x F x = F ' x = x 2 - 3 x 4 + 7

Como o termo de baixo é sempre positivo, porque é um termo elevado a um expoente par somado a um número positivo, só precisamos analisar o sinal do numerador:

x 2 - 3

Isso é uma parábola com concavidade para cima e raízes x = ± 3 .

Por isso, a gente pode dizer que essa derivada é negativa no intervalo - 3 ,   3 . Logo a função é decrescente nesse intervalo.

E podemos dizer que a derivada é positiva nos intervalos - ∞ ,   3 e 3 ,   + ∞ . Logo, a função é crescente nesses intervalos.

Passo 2

(b) Para ver a concavidade dessa função, precisamos analisar o sinal da derivada segunda:

F ' x = x 2 - 3 x 4 + 7

F ' ' x = 2 x   x 4 + 7 - 4 x 3 ( x 2 - 3 ) x 4 + 7 2 = - 2 x 5 + 12 x 3 + 14 x x 4 + 7 2

Como o denominador é sempre positivo por ser um termo elevado ao quadrado, só precisamos analisar o sinal do numerador:

- 2 x 5 + 12 x 3 + 14 x

Vamos fatorar ele:

- 2 x 5 + 12 x 3 + 14 x = - 2 x x 4 - 6 x 2 - 7 = - 2 x x 2 + 1 x 2 - 7

Daí a gente tira que essa expressão tem raízes em:

x = 0 ,   x = 7 ,   x = - 7

Passo 3

Agora precisamos testar o sinal de - 2 x 5 + 12 x 3 + 14 x nos intervalos:

- ∞ ,   - 7 ,   - 7 , 0 ,   0 , 7 ,   7 ,   + ∞

Fazendo isso, vemos que F ' ' x é positiva nos intervalos

- ∞ ,   - 7 ,   0 , 7

Logo, nesses intervalos a concavidade é para cima.

E nos intervalos

- 7 , 0 ,   7 ,   + ∞

A derivada segunda é negativa e a concavidade é para baixo.

Passo 4

(c) No passo 1, vimos que a derivada zera em x = ± 3 . Podemos usar o teste da derivada segunda para classificar esses pontos críticos.

Como x = - 3 está dentro do intervalo onde a derivada segunda é negativa, esse vai ser um ponto de máximo.

E como x = 3 está dentro do intervalo onde a derivada segunda é positiva, esse vai ser um ponto de mínimo.

Passo 5

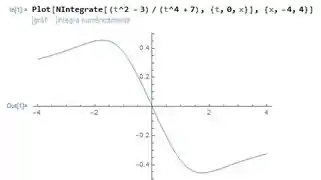
(d) Vamos usar o Wolfram Mathematica para fazer o gráfico. Fica assim:

Vemos que temos um máximo em - 3 ≈ - 1,7 e um mínimo em 3 ≈ 1,7 . E somente entre esses valores, a função é descrescente.

Vemos também que as concavidades mudam nos valores de x = ± 7 e x = 0 , conforme tínhamos dito antes.

Logo, tudo o que a gente calculou está certinho. 😊

Resposta

(a) Decrescente: - 3 ,   3 , Crescente: - ∞ ,   3 e 3 ,   + ∞ .

(b) Concavidade para cima: - ∞ ,   - 7 ,   0 , 7 , Concavidade para baixo: - 7 , 0 ,   7 ,   + ∞

(c) Máximo: x = - 3 e mínimo: x = 3

(d)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Use derivada para provar que a função é constante no intervalo ( 0 ,+ ∞ ) . F x = ∫ 0 x 1 1 + t 2 d t + ∫ 0 1 / x 1 1 + t 2 d t (b) Determine o valor constante da função na parte (a) e, então, int
Em cada parte, determine os valores de x com os quais F ( x ) é positiva, negativa ou zero, sem efetuar a integração. Explique seu raciocínio.(a) F x = ∫ 1 x t 4 t 2 + 3 d t (b) F x = ∫ - 1 x 4 - t 2
Use o gráfico de f abaixo para encontrar o valor médio def no intervalo [ 0 ,10 ] .
Encontre o valor médio de f ( x ) = e x + e - x acima do intervalo [ ln ⁡ 3 2 , ln ⁡ 2 ] .
Encontre uma função f e um número a tais que 2 + ∫ a x f ( t ) d t = e 3 x