Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.7 - Ex. 1
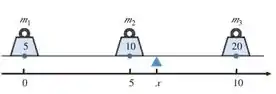
Conforme indica a figura ao lado, as massas e estão posicionadas numa certa viga sem peso.
- Suponha que o fulcro esteja posicionado em . Sem calcular a soma dos momentos em relação a , determine se essa soma é positiva, zero ou negativa. Explique.
- Onde deve ser colocado o fulcro para que a viga fique equilibrada?
Passo 1
(a) O enunciado quer que, só olhando a figura, a gente diga se a barra está girando e em que sentido. Repara que temos um peso sobre o ponto , a gente pode ignorar ele, porque ele não causa momento já que está logo em cima do ponto.
Olhando para os pesos das laterais, vemos que eles estão a mesma distância do ponto , mas o peso do lado direito é maior. Então nossa barrinha vai girar no sentido horário.
Passo 2
(b) Agora a gente pode somar os momentos de cada peso e igualar a zero para saber em que valor de há equilíbrio.
A soma dos momentos em torno da coordenada genérica fica:
Sendo:
Substituindo e isolando :
Resposta
(a) Resposta em texto nos passos.
(b)
Exercícios de Livros Relacionados
Use um CAS para encontrar a massa e o centro de gravidade da lâmina dada de densidade δ .A lâmina delimitada pelo gráfico de y = ln x , o eixo x e a reta x = 2 ; δ = 1 .
Use o Teorema de Pappus para calcular o volume do sólido gerado quando a região envolvida por y=x 2 e y=8-x 2 é girada em torno do eixo x .
Use o Teorema de Pappus para calcular o centroide da região triangular com vértices ( 0 ,0 ) ,( a ,0 ) e ( 0 ,b ) , onde a0 e b0 . [Sugestão: Gire a região em torno do eixo dos x para obter y - e em t
Suponha que uma região R do plano seja decomposta em duas regiões, R 1 e R 2 , cujas áreas sejam A 1 e A 2 , respectivamente, e cujos centroides sejam e ( x - 1 , y - 1 ) e ( x - 2 , y - 2 ) respectiv
Use o Teorema de Pappus e o resultado do Exercício 39 para calcular o volume do sólido gerado quando a região limitada pelo eixo x e o semicírculo y = a 2 - x 2 gira em torno da (b) reta y=x-a