Use o Teorema de Pappus para calcular o centroide da região triangular com vértices e onde e . [Sugestão: Gire a região em torno do eixo dos para obter e em torno do eixo dos para obter .]

Vamos começar descobrindo , girando a nossa região em torno de . Olha nossa região:

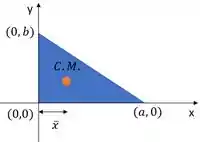
O trajeto que o centroide vai fazer é uma circunferência, que tem o raio igual à distância do próprio centroide ao eixo de rotação, o eixo . Pela figura, a gente vê que esse raio vale .

A distância percorrida pelo centroide é o comprimento dessa circunferência, que vale:

A área do triângulo que tem base e altura é:

O volume obtido pela rotação desse triângulo em torno de é um cone de raio e altura , logo o volume é:

Com tudo calculado, podemos usar:

Substituindo tudo que a gente tem na fórmula do teorema:

Isolando :

A gente faz a mesma coisa para mas girando o triângulo em torno do eixo :

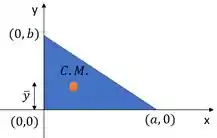
O raio da trajetória agora é a distância entre o centroide e o eixo , que vemos que vale . Logo o comprimento dessa trajetória, que é a distância percorrida pelo centroide, é:

A área do triângulo é a mesma:

Mas o volume muda. Ele é obtido pela rotação desse triângulo em torno de e é um cone de raio e altura , logo o volume é:

Com tudo calculado, podemos usar:

Substituindo tudo que a gente tem na fórmula do teorema:

Isolando :

Com tudo isso, vemos que o centroide está no ponto:

Ufa! Conseguimos!