Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.2 - Ex. 12bc
Considere a curva definida por
b) Dê uma equação cartesiana da curva
c) Esboce a curva
Passo 1
Pra gente conseguir a equação cartesiana vamos lembrar que
O truque de mestre vai ser sumir com o parâmetro. Pra isso, vamos focar em algo que eles tem em comum: o pedaço . Isolando esse pedaço na primeira equação, temos:
Usando isso na segunda equação:
Passo 2
A forma mais molezinha de esboçar a curva é a partir da equação cartesiana. Pra começar, note que quando , . Mas como toda boa exponencial, não temos a curva cortando o eixo . Então pra esboçar, é o suficiente fazer uma exponencial qualquer e por o intercepto e o ponto que o enunciado deu :
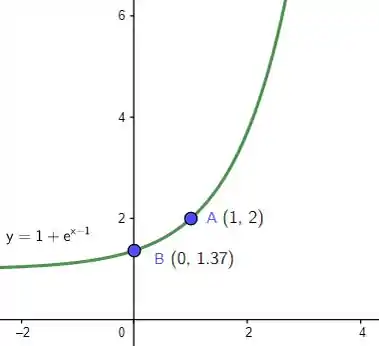
Resposta
b)
c) 
Exercícios de Livros Relacionados
Verificar que a curvavec r (t) = t c o s (t) vec i + t s e n (t) vec j + t vec k , t = 0 Está sobre um cone.
Se a = 4 b no exercício 7, temos uma hipociclóide de quatro cúspides ou astróide.
Uma hipociclóide é a curva traçada por um ponto P sobre uma circunferência de raio b que gira dentro de uma circunferência fixa de raio a , a ≥ b . Suponha que a origem é o centro da circunferência fi
Considere a curva definida por σ t = 1 + 2 ln 1 + t , 1 + 1 + t 2 ,t- 1 Determine uma equação da reta tangente à curva no ponto 1,2