30. Considere a equação
- Mostre que a Eq. (i) pode ser colocada na forma
logo, a Eq. (i) é homogênea.
(b) Introduza uma nova variável dependente υ de modo que υ = y/x, ou y = xυ(x). Expresse dy/dx em função de x, υ e dυ/dx.(c) Substitua y e dy/dx na Eq. (ii) pelas expressões no item (b) envolvendo υ e dυ/dx. Mostre que a equação diferencial resultante é
Ou
Note que a Eq. (iii) é separável.(d) Resolva a Eq. (iii) obtendo υ implicitamente em função de x.(e) Encontre a solução da Eq. (i) substituindo υ por y/x na solução encontrada no item (d).(f) Desenhe um campo de direções e algumas curvas integrais para a Eq. (i). Lembre-se de quea expressão à direita do sinal de igualdade na Eq. (i) depende, de fato, apenas da razão y/x.Isso significa que as curvas integrais têm a mesma inclinação em todos os pontos pertencentes auma mesma reta contendo a origem, embora essa inclinação varie de uma reta para outra.Portanto, o campo de direções e as curvas integrais são simétricos em relação à origem. Essapropriedade de simetria é evidente em seus gráficos?
Passo 1
Para o gráfico da função
Temos
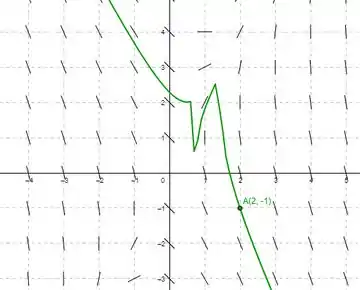
E para as curvas de solução temos esse gráfico
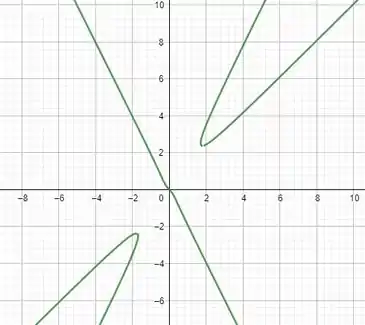
Terminamos por aqui, te vejo na próxima solução 😊
Resposta
Ei, a resposta está no passo a passo :)