(a) Use um sistema de computação algébrica para desenhar um campo de direções para a equação diferencial. Imprima-o e esboce algumas curvas solução sem resolver a equação diferencial.
(b) Resolva a equação diferencial.
(c) Use o SCA para desenhar vários membros da família de soluções obtida na parte (b). Compare com as curvas da parte (a).
Passo 1
(a) E aê, galera! Bora desenhar o campo de direções da equação diferencial:
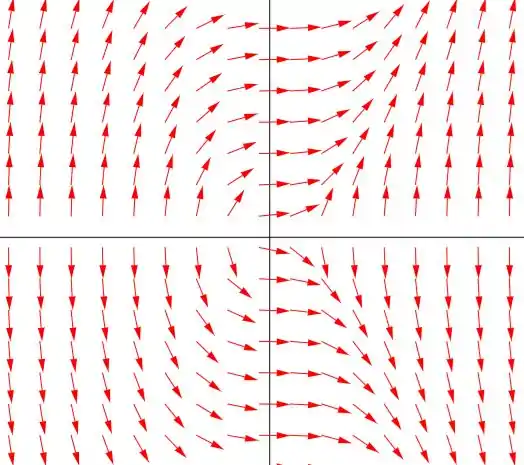
Passo 2
(b) Agora é resolver a equação, galera. Ela é separável, então só vamos passar o que é de pra um lado, o que é de pro outro, e integrar cada lado:
Passo 3
(c) Com a equação que a gente já encontrou no item anterior, podemos traçar uns gráficos legais dessa família de soluções. Quer ver?
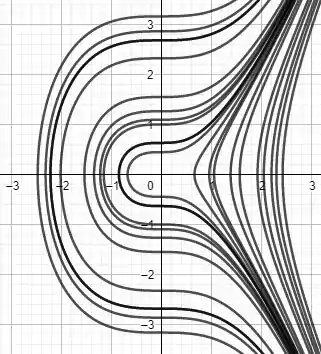
Agora olha de novo o campo de direções do item (a). Fala se não é super parecido?! É como se cada trajetória de setas fosse seguindo bonitinho uma curva da família de soluções.
Resposta
(b)