Considere a função . (Função maior inteiro.)
- Calcule , , e
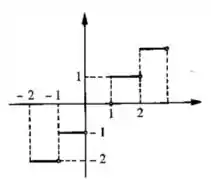
- Esboce o gráfico
Passo 1
- Para calcular vamos substituir no lugar de na função:
- Temos aqui o esboço do gráfico:
Temos que achar o valor máximo dentre o inteiros que seja menor que , no caso aqui seria o valor .
Vamos usar o mesmo raciocínio prar calcular, e :
Passo 2
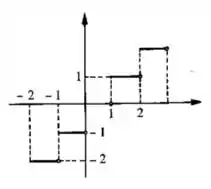
Resposta
- , , e