Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.6 - Ex. 67

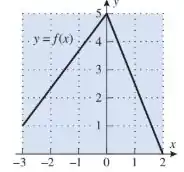
Considere a função f cujo gráfico está na figura abaixo. Calcule

d d x x + f x   x = - 1

Passo 1

Queremos calcular

d d x x + f x   x = - 1

Para tal, vamos começar derivando a função:

g x = f x + x

Podemos fazer isso a partir da regra da cadeia. Fazemos u = f x + x . Assim,

g ' x = d g d u d u d x

Passo 2

Assim,

g ' x = d d u u d d x f x + x g ' x = 1 2 u 1 2 - 1   f ' x + 1 g ' x = f ' x + 1 2 u

Lembrando que u = f x + x , segue que

g ' x = f ' x + 1 2 f x + x

Passo 3

Agora, vamos precisar encontrar como a função f se comporta. Note que f é a reunião de duas retas. Como queremos calcular g ' - 1 , vamos nos importar apenas com a reta que passa por x = - 1 !!

Lembre-se que a equação da reta que passa pelos pontos x 1 ,   y 1 e x 2 ,   y 2 é:

y - y 2 = y 2 - y 1 x 2 - x 1 x - x 2 A nossa reta passa por - 3,1 e 0,5 . Sendo assim,

f x - 5 = 5 - 1 0 - - 3 x - 0 f x = 4 3 x + 5

Sendo assim,

f ' x = 4 3

f - 1 = - 4 3 + 5 = 11 3

Passo 4

Com essas informações, temos:

g ' - 1 = f ' - 1 + 1 2 f - 1 - 1 g ' - 1 = 4 3 + 1 2 11 3 - 1 = 7 / 3 2 8 / 3 g ' - 1 = 7 / 3 4 2 / 3 g ' - 1 = 7 3 12 2 g ' - 1 = 7 6 24

Resposta

Temos d d x x + f x   x = - 1 = 7 6 24 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva as funções na forma y = f ( u ) e u = g ( x ) . Em seguida, determine d y / d x em função de x . y = 5 ⋅ cos - 4 ⁡ x
Escreva as funções na forma y = f ( u ) e u = g ( x ) . Em seguida, determine d y / d x em função de x . y = e 5 - 7 x
Escreva as funções na forma y = f ( u ) e u = g ( x ) . Em seguida, determine d y / d x em função de x . y = e 4 x + x 2
Escreva as funções na forma y = f ( u ) e u = g ( x ) . Em seguida, determine d y / d x em função de x . y = c o t g π - 1 x
Determine as derivadas das funções y = 2 r - r 2 3