Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.3 - Ex. 40
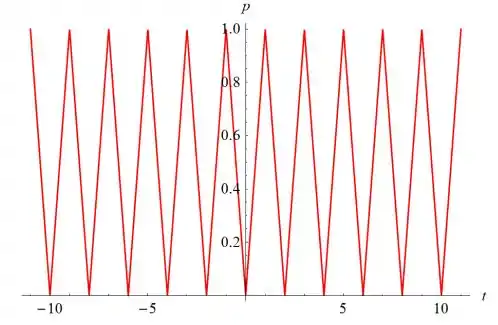
Considere a função p definida por:
- Esboce o gráfico de y = p(t).
- Encontre , notando que p é a extensão periódica da função h no Problema 39(c) e
- Encontre , observando que
usando, depois, o resultado do Problema 34.
em que f é a função no Problema 36, e usando, depois, o Teorema 6.2.1.
Passo 1
Na letra a, o gráfico será:
Passo 2
Na letra b, como p (t) é periódico, podemos usar a fórmula derivada no Problema 34 para determinar sua transformada de Laplace. O período aqui é T=2.
Resolvendo essas duas integrais, teremos:
Passo 3
Agora, na letra c temos a seguinte função:
Diferencie os dois lados em relação a t.
Faça a transformação de Laplace de ambos os lados.
Use o fato de que a derivada se transforma como
Então:
E chegamos em:
Passo 4
Foi encontrado no Problema 36 que:
Portanto, como p (0) = 0,
Resposta
Exercícios de Livros Relacionados
Suponha que f satisfaz f(t + T) = f(t) para todo t ≥ 0 e para algum número positivo fixo T; f édita periódica com período T em 0 ≤ t ∞. Mostre que ℒ { f ( t ) } = ∫ 0 T e - s t f ( t ) d t 1 - e - s T
Use os resultados do Problema 25 para encontrar a transformada de Laplace inversa da função dada. F ( s ) = 2 s + 1 4 s 2 + 4 s + 5
Use o resultado do Problema 34 para encontrar a transformada de Laplace da função dada. f ( t )=1 ,0 ≤ t1 f ( t ) =- 1 ,1 ≤ t2 ; f ( t + 2 )=f ( t ) função f ( t )
Use o resultado do Problema 34 para encontrar a transformada de Laplace da função dada. f ( t )=1 ,0 ≤ t1 f ( t ) =0 ,1 ≤ t2 ; f ( t + 2 )=f ( t )
Encontre a transformada de Laplace da função dada. f ( t ) = 0 ,0 ≤ t1 f ( t ) = 1 ,t ≥ 1