Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 5
Considere a função .
a) Mostre que
b) Esboce o gráfico de .
Passo 1
Fala pessoal, tudo certo? Nessa questão, temos uma função com módulos:
Mas quem exatamente é essa função? Bem, pra sabermos, vamos ter que lembrar da definição de módulo, ok? Ela vai ser:
Nosso objetivo é Mostrar que
E Esboçar o gráfico de .
E aí a gente aplica essa definição pros nossos casos. Partiu?
Passo 2
Pra começar, temos . Pela definição de módulo, vamos ter:
Podemos escrever assim,
Vamos representar essa região graficamente!
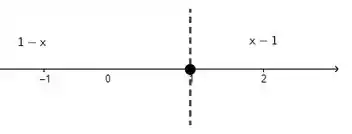
Note que no lado esquerdo vale a expressão , e no lado direito a expressão .
Vamos fazer a mesma coisa para . Fica assim,
Podemos escrever assim,
Traçando a região que cada expressão representa ficamos com
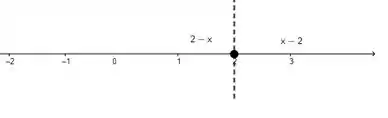
Agora vamos juntar as duas representações! Como nossa função é um módulo mais o outro, podemos usar a reta real pra nos ajudar a ver o resultado:
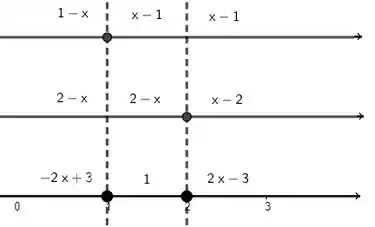
Resumindo o que quis mostrar foi,
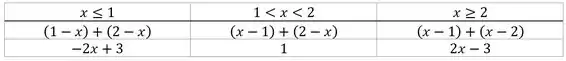
E pronto! Tá provado que:
Passo 3
O gráfico de então, é composto por três retas (como definida nas regiões do passo anterior).
Para , temos
Para , temos a reta constante
Para , teremos
Logo, seu esboço é:
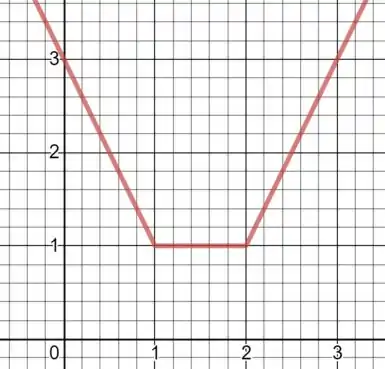
Resposta
Resposta nos passos