Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.5 - Ex. 9
9 - Considere o problema de valor inicial e , com e.
A generalização do método de previsão e correção de Adam-Moulton da Seção 8.4 é
e
Determine um valor aproximado da solução em para o problema de valor inicial do exemplo, ,
Com . Use. Corrija o valor previsto uma vez. Para os valores , use os valores da solução exata arredondados para seis dígitos:;;;; e
Passo 1
Dado que o problema do valor inicial é,
com . A generalização do método nos fornece:
Que após a correção tornam-se:
Agora iremos usar os valores iniciais da solução exata, para obter:
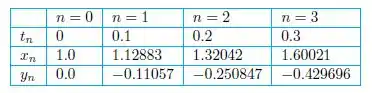
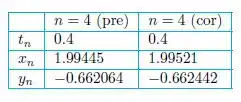
Finalmente, iremos utilizar uma única etapa por meio do método previsão e correção, que resulta em valores aproximados:
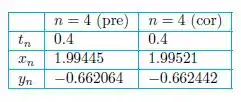
Você vai notar que os valores de e usando os métodos previsão e correção são bastante próximos, como eles só diferem na 3ª casa decimal.
Resposta
