Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.7 - Ex. 19
Considere o problema de valor inicial
em que é um número dado.
- Desenhe um campo de direções para a equação diferencial. Observe que existe um valor critico de no intervalo de que separa as soluções convergentes das divergentes. Chame esse valor critico de
- Use o método de Euler com para estimar . Faça isto restringindo a um intervalo [a, b] em que
Passo 1
Para resolvermos esse problema, vamos usar o método de Euler, que consiste em um calculo numérico para as equações em que não temos um valor exato, onde o resultado se aproxima cada vez mais do exato de acordo com o passo usado para o calculo.
Passo 2
- Temos que o campo é divergente e muito parecido com a imagem a seguir
- Utilizando o método de Euler, temos que a equação usada é dada por
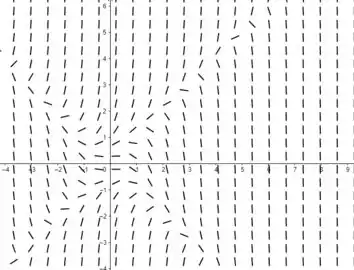
Como dito no enunciado, nosso ponto critico fica entre 0 e 1, onde podemos observar que há uma certa divergência no campo.
Passo 3
Se testarmos alguns valores entre e , com a ajuda de um software, para o dado, podemos ver que o valor de para um que varia de será de aproximadamente . Para qualquer valor de acima de as soluções começam a divergir.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Uma partícula move-se ao longo de uma linha reta, em t segundos, s é a distância orientada da partícula até a origem, v m/s é a sua velocidade e a m/s² é a sua aceleração. (21) v = 2 t + 4s ; s = 0 q
Uma partícula move-se ao longo de uma linha reta, em t segundos, s é a distância orientada da partícula até a origem, v m/s é a sua velocidade e a m/s² é a sua aceleração. (22) v = 4 - ts ; s = 0 q u
Uma partícula move-se ao longo de uma linha reta, em t segundos, s é a distância orientada da partícula até a origem, v m/s é a sua velocidade e a m/s² é a sua aceleração. (23) a = 5 - 2 ts ; v = 2es
Um peso de 96n e w t o n s desliza por um plano inclinado, fazendo um ângulo de 30 ° com a horizontal. Se o coeficiente de atrito é μ , determine a equação diferencial para a velocidade v ( t ) do pes
O tanque cônico, mostrado na figura 1.26, derrama água por um orifício no fundo. Se a área da seção transversal do orifício é 1 4 m ² ², encontre a equação diferencial que representa a altura da água