Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 1.Exercícios de Revisão - Ex. 20

Um peso de 96   n e w t o n s desliza por um plano inclinado, fazendo um ângulo de 30 ° com a horizontal. Se o coeficiente de atrito é μ , determine a equação diferencial para a velocidade v ( t ) do peso no instante t . Considere o fato de que a força de atrito no sentido oposto ao movimento é μ N , em que N é a componente normal do peso. Veja a figura 1.27.

Passo 1

Humm beleza, temos um peso de 96   n e w t o n s deslizando em um plano inclinado, de acordo com o esquema:

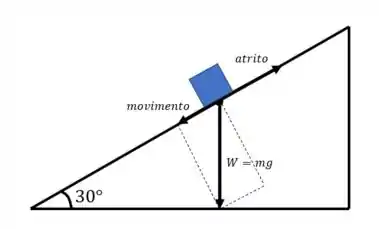
E aí queremos encontrar a equação diferencial da velocidade no instante t , ou seja: queremos d v d t

Para isso vamos usar a segunda lei de Newton, beleza? Bora lá!

Passo 2

Da segunda lei de Newton, temos

F = m . a

Então temos

m . a = m . g . s e n 30 ° - μ N . c o s ⁡ ( 30 ° )

Porém, N , que é a força normal, é justamente igual m . g

Além disso, temos que a aceleração é a derivada da velocidade, então:

m . d v d t = m . g . s e n 30 ° - μ . m . g . c o s ⁡ ( 30 ° )

Então:

d v d t = g . 1 2 - μ . g . 3 2

Substituindo g por 10   m / s ² :

d v d t = 5 - 5 3 μ

Resposta

d v d t = 5 - 5 3 μ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A segunda lei de Newton F = m . a pode ser escrita como F = d d t ( m . v ) . Quando a massa de um objeto não é constante, esta última formulação é usada. A massa m ( t ) de um foguete muda enquanto s
Uma pessoa P, partindo da origem, move-se na direção positiva do eixo x, puxando um peso ao longo da curva C (chamada tratriz), como mostrado na figura 1.24. O peso, inicialmente localizado no eixo y
Uma curva C no plano reflete os raios de luz de tal modo que todo raio L paralelo ao eixo y é refletido para um único ponto 0. Determine a equação diferencial para a função y = f ( x ) que descreve a
Determine as equações do movimento se o projétil no Problema 12 encontrar uma força de retardamento k (de magnitude k ) agindo tangencialmente à trajetória mas, oposta ao movimento. Veja a Figura 1.21
No Problema 21, suponha que a quantidade de material esquecida é proporcional à quantidade memorizada no instante t . Qual é a equação diferencial para A quando o esquecimento é levado em conta?