Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 3.7 - Ex. 25b

Considere o problema de valor inicial.

Queremos explorar quão longo é o intervalo de tempo necessário para que a solução se torne “desprezível” e como esse intervalo depende do coeficiente de amortecimento γ. Mais precisamente, vamos procurar o instante τ tal que |s(t)| τ. Note que o amortecimento crítico para este problema ocorre quando γ = 2.

Repita o item (a) para diversos outros valores de γ no intervalo 0

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos a solução para a equação. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser relembrar que temos a seguinte relação:

u = e r t

u ' = r e r t

u ' ' = r ² e r t

A amplitude do sistema é dada por:

r 2 e r t + γ r e r t +   e r t = 0

r ² + γ r + 1 = 0

r = - γ 2 ± i μ  

u t = e - γ t 2 2 cos ⁡ 4 - γ 2 2 t + 2 γ 4 - γ 2 sin ⁡ 4 - γ 2 2 t

Passo 3

Pronto!! Agora é só substituir os valores e achar a solução!!

...

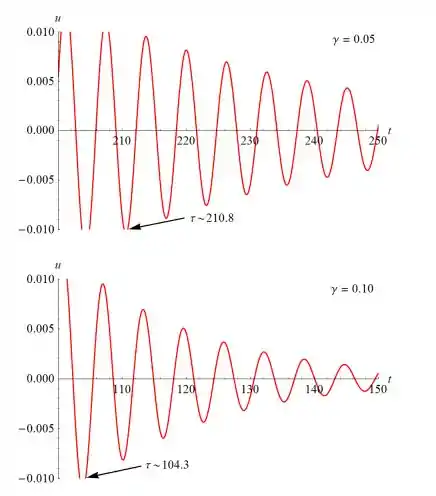
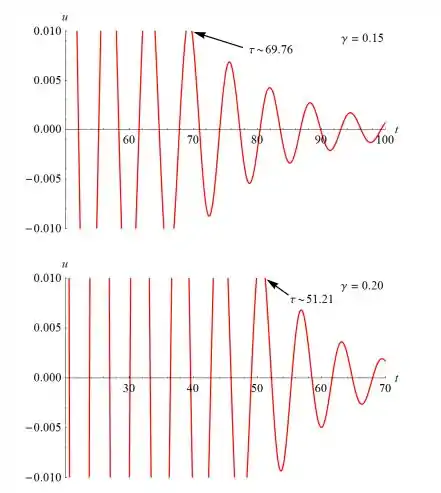
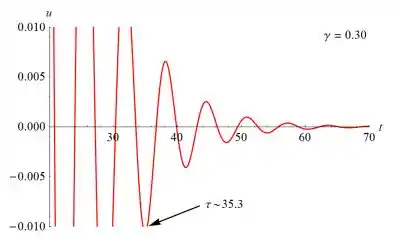
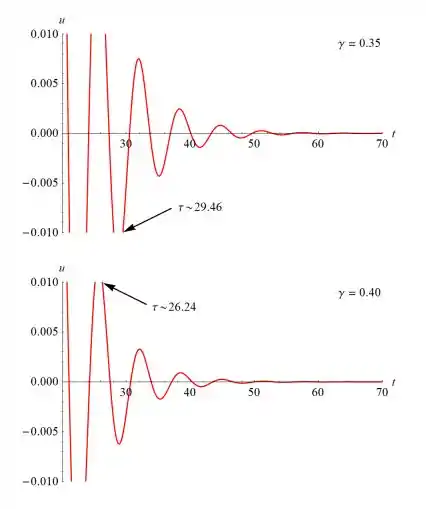Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a equação (17) para mostrar que o gráfico de x t = A . e - λ t . s e n ω 2 - λ 2 t + θ intercepta o eixo t exatamente no valor médio dos instantes nos quais o gráfico de x ( t ) toca os gráficos d
O decremento logarítmico definido no problema 23 é um indicador da taxa em que o movimento está sendo amortecido.(a) Descreva o movimento de um sistema subamortecido se δ for um número positivo muito
Uma massa de 1 kg é atada a uma mola cuja constante é 16 N/m. Uma força externa igual a f t = 8 . s e n ( 4 t ) age no sistema a partir de t = 0 . Encontre a equação de movimento se o meio oferece uma
Uma massa de 2kg é atada a uma mola cuja constante vale 32 N/m. Uma força igual a f t = 68 . e - 2 t . c o s ⁡ ( 4 t ) atua no sistema a partir de t = 0 . Encontre a equação de movimento na ausência d
No problema 5, escreva a equação de movimento na forma x t = A . s e n ω t + ϕ + B . e - 2 t . s e n ( 4 t + θ ) . Qual é a amplitude de vibrações após um longo período de tempo?