Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.4 - Ex. 23

Considere o problema de valor inicial

y ' ' + y = h ( t ) ,   y ( 0 ) = 0 ,   y ' ( 0 ) = 0

em que

h ( t ) = u 0 ( t ) + 2 ∑ k = 1 n ( - 1 ) k u 11 k / 4 ( t ) .

Observe que esse problema é idêntico ao Problema 19, exceto que a frequência do termo não

homogêneo foi um pouco aumentada.

  1. Encontre a solução desse problema de valor inicial.
  2. Seja n ≥ 33 e desenhe o gráfico da solução para um intervalo 0 ≤ t ≤ 90 ou maior. Seu gráfico deve mostrar um batimento claramente reconhecível.
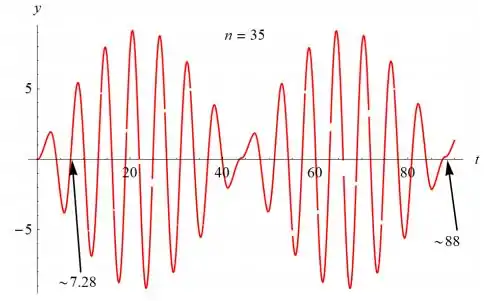
  3. Do gráfico no item (b), estime o “período lento” e o “período rápido” para esse oscilador.
  4. Para um oscilador sob a ação de uma força senoidal, mostramos, na Seção 3.8, que a “frequência lenta” é dada por ω - ω 0 / 2 , em que ω 0 é a frequência natural do sistema e ω é a frequência do termo não homogêneo. Analogamente, a “frequência rápida” é ω - ω 0 / 2 . Use essas expressões para calcular o “período rápido” e o “período lento” para o oscilador nesse problema. Quão próximos esses resultados estão de suas estimativas no item (c)?

Passo 1

Como a EDO é linear, a transformação de Laplace pode ser aplicada para resolvê-lo. A transformada de Laplace de uma função y(t) é definida aqui como:

Y ( s )   =   ℒ { y ( t ) } = ∫ 0 ∞ e - s t y ( t )   d t

Consequentemente, a primeira e a segunda derivadas se transformam da seguinte maneira.

ℒ { d y d t } = s Y ( s )   -   y ( 0 )

ℒ { d ² y d t ² } = s ² Y ( s )   -   s y ( 0 ) - y ' ( 0 )

Aplique a conversão Laplace nos dois lados da EDO:

ℒ { y ' ' + y } = ℒ { u 0 ( t ) + 2 ∑ k = 1 n ( - 1 ) k u 11 k / 4 ( t ) }

ℒ { y ' ' } + ℒ { y } = ℒ { u 0 ( t ) } + 2 ∑ k = 1 n ( - 1 ) k ℒ { u 11 k / 4 ( t ) }

s ² Y ( s )   -   s y ( 0 ) - y ' ( 0 ) + Y ( s ) = ∫ 0 ∞ e - s t u 0 ( t ) d t   +   2 ∑ k = 1 n ( - 1 ) k ∫ 0 ∞ e - s t u 11 k / 4 ( t ) d t

Passo 2

Aplique as condições iniciais, y ( 0 ) = 0 e y ' ( 0 ) = 0 .

( s ² + 1 ) Y ( s ) = 1 s + 2 ∑ k = 1 n ( - 1 ) k ( e - 11 k s / 4 s )

Como resultado da aplicação da transformada de Laplace, a EDO reduziu a uma equação algébrica para Y, (a solução transformada):

Y ( s ) = ( 1 s - s s ² + 1 ) + 2 ∑ k = 1 n ( - 1 ) k ( 1 s - s s 2 + 1 ) e - 11 k s / 4

Passo 3

Agora, basta resolver esta equação e achar sua inversa, chegando em:

y ( t ) = ℒ - 1 { Y ( s ) } = 1 - c o s ( t )   + 2 ∑ k = 1 n ( - 1 ) k [ 1 - c o s ( t - 11 k / 4 ) ] u 11 k / 4 ( t )

Abaixo está um gráfico de y (t) versus t para n = 35:

B a i x a   f r e q u ê n c i a :   | ω - ω 0 | 2 = 0.0712

A l t a   f r e q u ê n c i a :   ω + ω 0 2 = 1.07

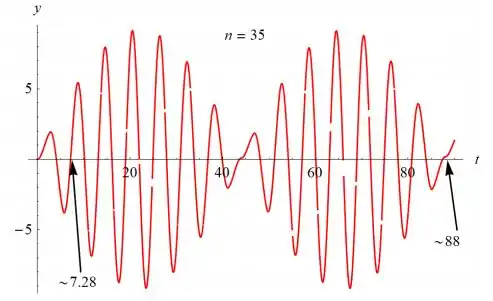
Agora calcule as diferenças percentuais para ver a que distância esses resultados estão das estimativas.

B a i x a   f r e q u ê n c i a :   π 44 - 4 π - 11 22 4 π - 11 22 = 0.283 %

A l t a   f r e q u ê n c i a :   25 π 91 - 4 π + 11 22 4 π + 11 22 = - 19.4 %

Portanto, a estimativa medida para a frequência lenta é 0,283% maior que a calculada

e a estimativa medida para a frequência rápida é 19,4% menor que o valor calculado

Resposta

  1. y ( t ) = ℒ - 1 { Y ( s ) } = 1 - c o s ( t )   + 2 ∑ k = 1 n ( - 1 ) k [ 1 - c o s ( t - 11 k / 4 ) ] u 11 k / 4 ( t )
  3. B a i x a   f r e q u ê n c i a :   | ω - ω 0 | 2 = 0.0712

    4. A l t a   f r e q u ê n c i a :   ω + ω 0 2 = 1.07

  4. B a i x a   f r e q u ê n c i a :   π 44 - 4 π - 11 22 4 π - 11 22 = 0.283 %

A l t a   f r e q u ê n c i a :   25 π 91 - 4 π + 11 22 4 π + 11 22 = - 19.4 %

Portanto, a estimativa medida para a frequência lenta é 0,283% maior que a calculada e a estimativa medida para a frequência rápida é 19,4% menor que o valor calculado

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Modifique o problema no Exemplo 2 desta seção substituindo o termo não homogêneo g(t) por f ( t ) = u 5 ( t ) - ( t - 5 ) - u 5 + k ( t ) ( t - 5 - k ) k Esboce o gráfico de f(t) e descreva como ele d
Considere o problema de valor inicial y ' ' + 0.1 y ' + y = f ( t ) ,y ( 0 ) = 0 ,y ' ( 0 ) = 0 em que f(t) é a mesma que no Problema 19.Desenhe o gráfico da solução. Use um valor de n suficientemente
Considere o problema de valor inicial y ' ' + y = f ( t ) ,y ( 0 ) = 0 ,y ' ( 0 ) = 0 em que f ( t ) = u 0 ( t ) + 2 ∑ k = 1 n ( - 1 ) k u k π ( t ) . Desenhe o gráfico de f(t) em um intervalo como 0
Considere o problema de valor inicial y ' ' + 1 3 y ' + 4 y = f k ( t ) ,y ( 0 ) = 0 ,y ' ( 0 ) = 0 . em que f k ( t ) = 1 2 k ,4 - k ≤ t4 + k f k ( t ) = 0 ,0 ≤ t4 - k et ≥ 4 + k e 0 Esboce o gráfico