Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.4 - Ex. 19
Considere o problema de valor inicial
em que
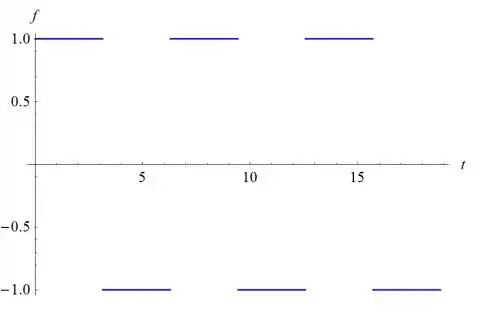
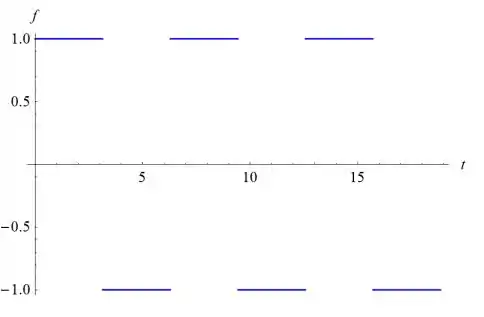
- Desenhe o gráfico de f(t) em um intervalo como 0 ≤ t ≤ 6π.
- Encontre a solução do problema de valor inicial.
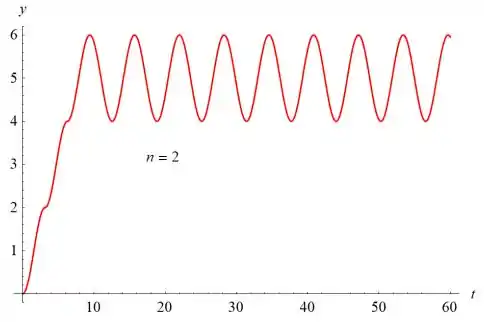
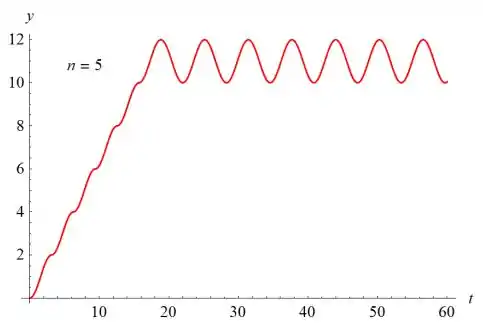
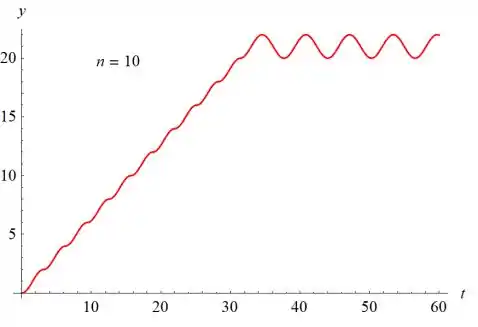
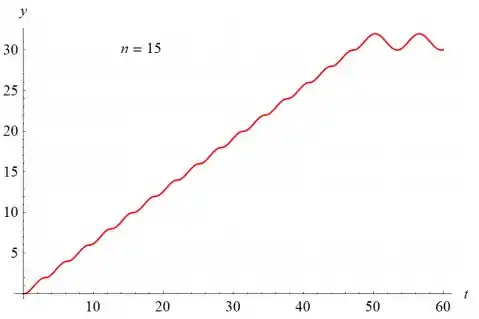
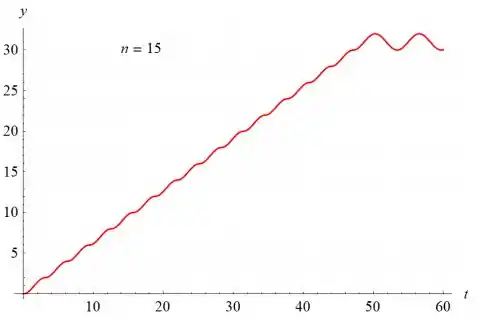
- Seja n = 15 e desenhe o gráfico da solução para 0 ≤ t ≤ 60. Descreva a solução e explique por que ela se comporta dessa maneira.
- Investigue como a solução varia quando n aumenta. O que acontece quando n → ?
Passo 1
No intervalo 0 ≤ t ≤ 6π, é diferente de zero se k
Passo 2
Como a EDO é linear, a transformação de Laplace pode ser aplicada para resolvê-lo. A transformada de Laplace de uma função y(t) é definida aqui como:
Consequentemente, a primeira e a segunda derivadas se transformam da seguinte maneira.
Aplique a conversão Laplace nos dois lados da EDO:
Passo 3
Aplique as condições iniciais, e .
Como resultado da aplicação da transformada de Laplace, a EDO reduziu a uma equação algébrica para Y, (a solução transformada):
Passo 4
Agora, basta resolver esta equação e achar sua inversa!
Chegando em:
Passo 5
Na letra c:
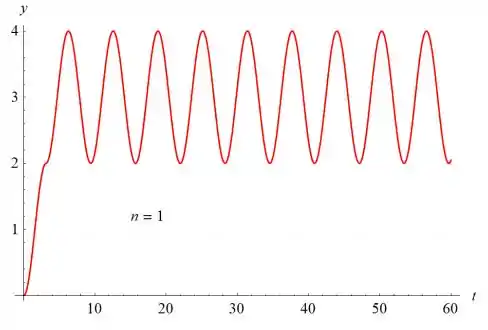
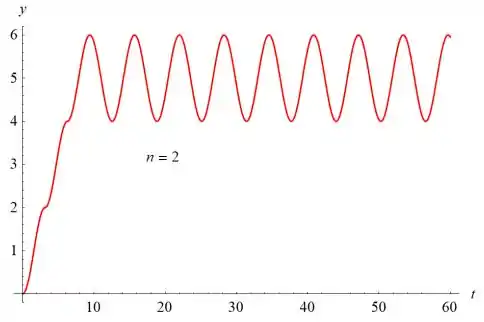
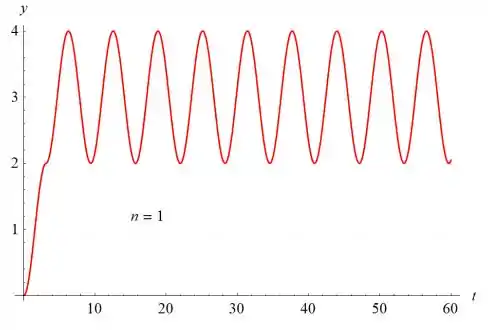
Os gráficos de y (t) versus t são mostrados abaixo para n = 1, n = 2, n = 5, n = 10 e n = 15.
Passo 6
Na letra d:
O valor de n determina o número de sulcos à medida que o gráfico aumenta. O gráfico oscila com uma amplitude de 1 e um período de sobre o valor . Se , o gráfico cresce a uma taxa linear para sempre.
Resposta
- O valor de n determina o número de sulcos à medida que o gráfico aumenta. O gráfico oscila com uma amplitude de 1 e um período de sobre o valor . Se , o gráfico cresce a uma taxa linear para sempre.
