Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.4 - Ex. 18

Considere o problema de valor inicial

y ' ' + 1 3 y ' + 4 y = f k ( t ) ,   y ( 0 ) = 0 ,   y ' ( 0 ) = 0 .

em que

f k ( t ) = 1 2 k ,   4 - k ≤ t < 4 + k

f k ( t ) = 0 ,   0 ≤ t < 4 - k     e       t ≥ 4 + k

e 0

  1. Esboce o gráfico de f k ( t ) . Note que a área sob o gráfico é independente de k. No caso em que f k ( t ) representa uma força, isto significa que o produto do módulo da força e do intervalo de tempo durante o qual ela age não depende de k.
  2. Escreva f k ( t ) em termos da função degrau unitário e depois resolva o problema de valor inicial dado.
  3. Desenhe o gráfico da solução para k = 2, k = 1 e k = 1/2. Descreva como a solução depende de k.

Passo 1

Na letra a:

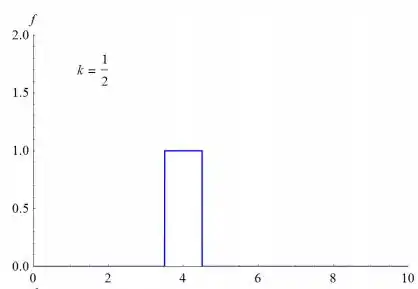
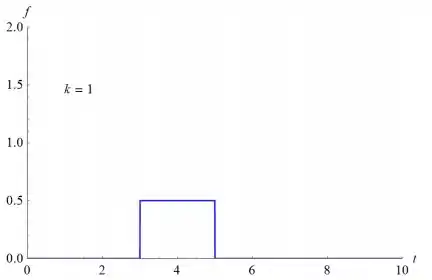
Passo 2

Na letra b:

Para fazer com que a função tenha o valor 1/2k em t = 4 - k, use a função Heaviside H[t-(4-k)], definida como 1 se t> 4 - ke 0 se t 4 + k.

f k ( t ) = 1 2 k H [ t - ( 4 - k ) ] - 1 2 k H [ t - ( 4 + k ) ] = 1 2 k [ u 4 - k ( t )   -   u 4 + k ( t ) ]

O problema do valor inicial a ser resolvido é

y ' ' + 1 3 y ' + 4 y = 1 2 k [ u 4 - k ( t ) - u 4 + k ( t ) ] ,       y ( 0 ) = 0 ,   y ' ( 0 ) = 0 .

Como a EDO é linear, a transformação de Laplace pode ser aplicada para resolvê-lo. A transformada de Laplace de uma função y(t) é definida aqui como:

Y ( s )   =   ℒ { y ( t ) } = ∫ 0 ∞ e - s t y ( t )   d t

Consequentemente, a primeira e a segunda derivadas se transformam da seguinte maneira.

ℒ { d y d t } = s Y ( s )   -   y ( 0 )

ℒ { d ² y d t ² } = s ² Y ( s )   -   s y ( 0 ) - y ' ( 0 )

Aplique a conversão Laplace nos dois lados da EDO:

ℒ { y ' ' + 1 3 y ' + 4 y } = ℒ { 1 2 k [ u 4 - k ( t )   -   u 4 + k ( t ) ] }

ℒ { y ' ' } + ℒ { 1 3 y ' } + ℒ { 4 y } = 1 2 k ℒ { u 4 - k ( t ) } - 1 2 k ℒ { u 4 + k ( t ) }

[ s ² Y ( s )   -   s y ( 0 ) - y ' ( 0 ) ] + 1 3 [ s Y ( s )   -   y ( 0 ) ] + 4 Y ( s ) = 1 2 k ∫ 0 ∞ e - s t [ u 4 - k ( t ) ] d t - 1 2 k ∫ 0 ∞ e - s t [ u 4 + k ( t ) ] d t

Passo 3

Aplique as condições iniciais, y ( 0 ) = 0 e y ' ( 0 ) = 0 ,

s ² Y ( s ) + 4 Y ( s ) = 1 s ² + 1 + 1 s ² + 1 e - π s

Como resultado da aplicação da transformada de Laplace, a EDO reduziu a uma equação algébrica para Y, (a solução transformada):

s ² Y ( s ) + 1 3 s Y ( s ) + 4 Y ( s ) = 1 2 k ∫ 4 - k ∞ e - s t d t - 1 2 k ∫ 4 + k ∞ e - s t d t

Y ( s ) = 1 2 k [ 1 4 s - 1 4 s + 1 6 ( s + 1 6 ) 2 + 143 36 - 1 4 143 143 6 ( s + 1 6 ) ² + 143 36 ] e - ( 4 + k ) s

Passo 4

Agora, basta resolver esta equação e achar sua inversa!

y ( t ) = ℒ - 1 { Y ( s ) } = ℒ - 1 { 1 2 k [ 1 4 s - 1 4 s + 1 6 ( s + 1 6 ) 2 + 143 36 - 1 4 143 143 6 ( s + 1 6 ) ² + 143 36 ] e - ( 4 + k ) s }

Chegando em:

y ( t ) = 1 8 k { 1 - e - ( t - 4 - k ) / 6 c o s [ 143 6 ( t - 4 + k ) ] - 1 143 e - ( t - 4 - k ) / 6 s e n [ 143 6 ( t - 4 + k ) ] } u 4 - k ( t )

- 1 8 k { 1 - e - ( t - 4 - k ) / 6 c o s [ 143 6 ( t - 4 - k ) ] - 1 143 e - ( t - 4 - k ) / 6 s e n [ 143 6 ( t - 4 - k ) ] } u 4 + k ( t )

Passo 5

Na letra c:

Abaixo estão os gráficos para y (t) versus t para k = 1/2, k = 1, k = 2 e k=10.

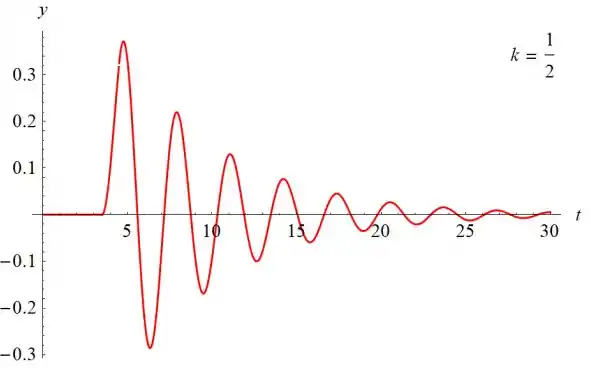
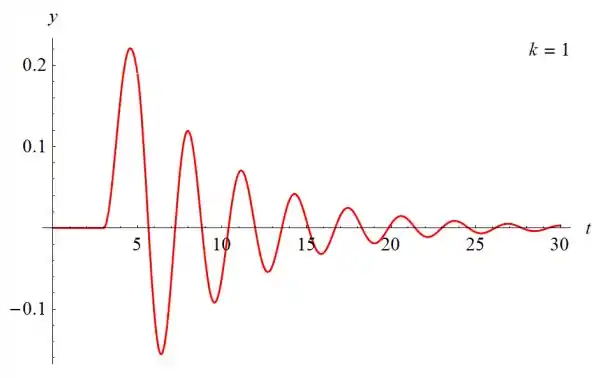
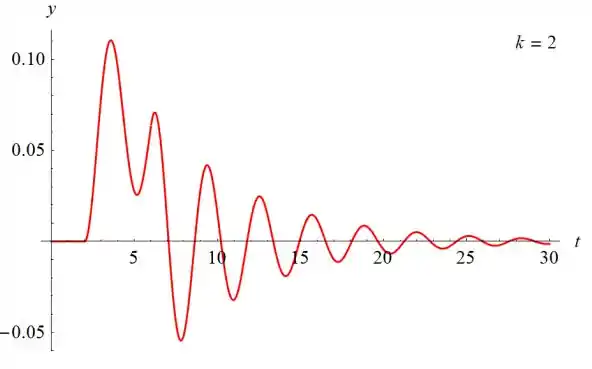
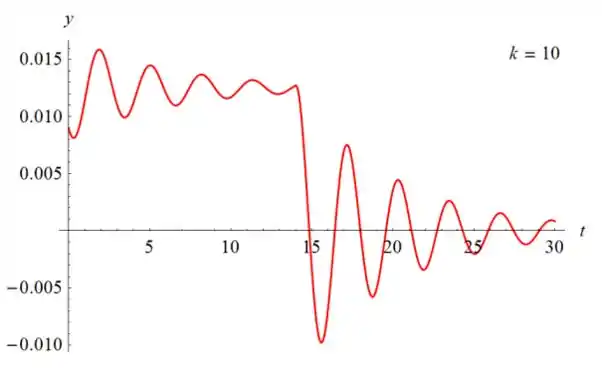
À medida que k aumenta, a amplitude de y (t) diminui. Inicialmente, o gráfico se aproxima do eixo y e, eventualmente, se eleva acima do eixo t.

Resposta

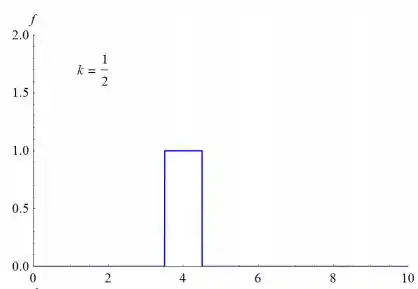
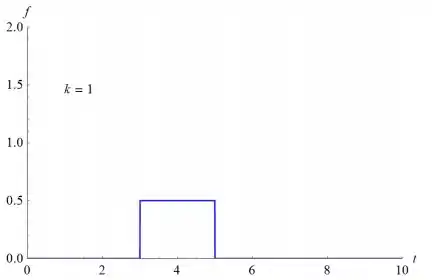
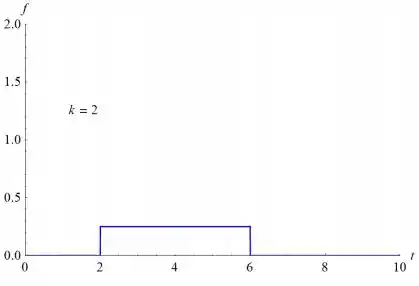
  2. y ( t ) = 1 8 k { 1 - e - ( t - 4 - k ) / 6 c o s [ 143 6 ( t - 4 + k ) ] - 1 143 e - ( t - 4 - k ) / 6 s e n [ 143 6 ( t - 4 + k ) ] } u 4 - k ( t )

    3. - 1 8 k { 1 - e - ( t - 4 - k ) / 6 c o s [ 143 6 ( t - 4 - k ) ] - 1 143 e - ( t - 4 - k ) / 6 s e n [ 143 6 ( t - 4 - k ) ] } u 4 + k ( t )

  3. À medida que k aumenta, a amplitude de y (t) diminui. Inicialmente, o gráfico se aproxima do eixo y e, eventualmente, se eleva acima do eixo t.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre uma expressão envolvendo u c ( t ) para uma função g cujo gráfico é uma rampacrescente de zero em t = t 0 até o valor h em t = t 0 + k , seguida de uma rampa decrescente quechega a zero em t
Encontre a solução do problema de valor inicial dado.Desenhe os gráficos da solução e do termo não homogêneo; explique a relação entre eles. y ' ' + y=u 3 π ( t ) ; y ( 0 ) = 1 ,y ' ( 0 ) = 0
Encontre a solução do problema de valor inicial dado.Desenhe os gráficos da solução e do termo não homogêneo; explique a relação entre eles. y ' '+ 4 y=s e n ( t )- u 2 π ( t )s e n ( t - 2 π ) ;y ( 0
Encontre a solução do problema de valor inicial dado.Desenhe os gráficos da solução e do termo não homogêneo; explique a relação entre eles. y ' ' + y ' + 5 4 y = g ( t ) ;y ( 0 ) = 0 ,y ' ( 0 ) = 0 ;
Determinado sistema mola-massa satisfaz o problema de valor inicial u ' ' + 1 4 u ' + u = k g ( t ) ,u ( 0 ) = 0 ,u ' ( 0 ) = 0 , em que g ( t ) = u 3 / 2 ( t ) - u 5 / 2 ( t ) e k0 é um parâmetro.Esb