Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 67
- Qual é a distância mínima da curva ao ponto ? (Dica: minimizando o quadrado da distância, você evita trabalhar com raízes quadradas.)
- Trace o gráfico da função distância D(x) juntamente com o de e concilie o que você observa com a resposta do item (a)
Passo 1
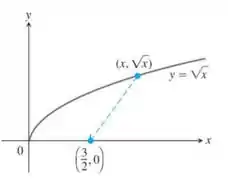
O problema quer que calculemos a distância mínima da curva ao ponto dados, além disso, dá uma dica para evitar trabalhar com raiz quadrada que é minimizar o quadrado da distância (que vem da fórmula da distância entre 2 pontos: ). Por fim, pede pra traçar a curva dada juntamente com a função que encontramos resolvendo o item (a).
Passo 2
Os pontos que pertencem à curva são pontos do tipo . Adotando a função como sendo a função que representa o quadrado da distância, como a dica nos sugere, utilizando a distância entre dois pontos teremos
Para função do segundo grau, sabemos que seu valor máximo/mínimo absoluto se encontra no vértice, para tal basta fazermos
Portanto, nossa função tem valor mínimo quando . Assim, a distância mínima será dada por .
Finalmente,
Passo 3
Plotando os 2 gráficos obtemos
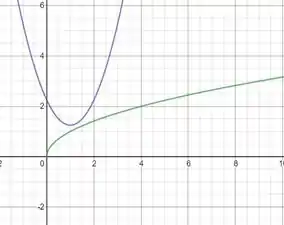
A distância mínima do ponto ao ponto no gráfico de ocorre quando e nossa função assume seu valor mínimo.
Resposta
Ei, a resposta está no passo a passo :)