Considere o sistema com duas massas e três molas cujas equações de movimento são as Eq.
(22) no texto. Suponha que .
(a) Como no texto, transforme o sistema em quatro equações de primeira ordem da forma . Determine a matriz de coeficientes .
(b) Encontre os autovalores e autovetores de .
(c) Escreva a solução geral do sistema.
(d) Descreva os modos fundamentais de vibração. Para cada modo fundamental, desenhe gráficos de y1 e de y2 em função de t. Desenhe, também, as trajetórias correspondentes nos planos y1y3 e y2y4.
(e) Considere as condições iniciais . Calcule as constantes arbitrárias na
solução geral do item (c). Qual é o período do movimento nesse caso? Desenhe gráficos de y1 e de y2 em função de t. Desenhe, também, as trajetórias correspondentes nos planos y1y3 e y2y4. Certifique-se de que você compreende como as trajetórias são percorridas durante um período completo.
(f) Considere outras condições iniciais de sua escolha e desenhe gráficos semelhantes aos
pedidos no item (e).
Passo 1
e) temos que este exercício aqui é exatamente igual ao item (e), mas com valores iniciais diferentes a nossa escolha. Eu estarei escolhendo estes aqui:
Trazendo da solução do item (c):
Aplicando , temos:
E teremos o seguinte sistema:
Resolvendo este sistema, por meio de substituição, temos as seguintes soluções:
E quesito o período será de , pois e possuem períodos de e e possuem um período de e dois períodos se encontram em .
Passo 2
Após o calculo do problema de valor inicial, temos que desenhar os gráficos das soluções, vamos lá.
Gráfico de :
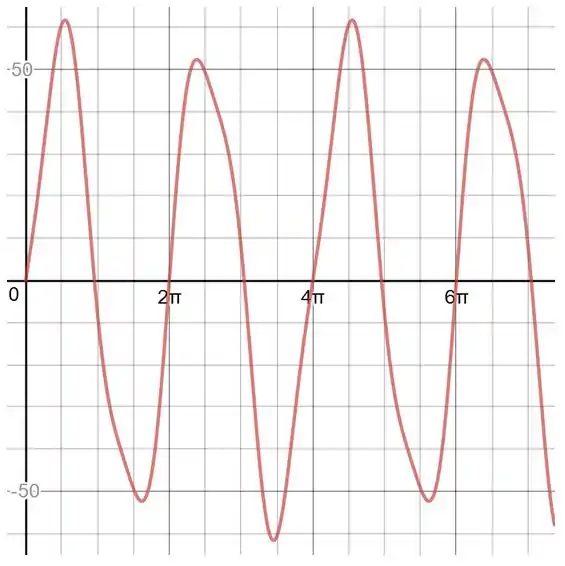
Gráfico de :
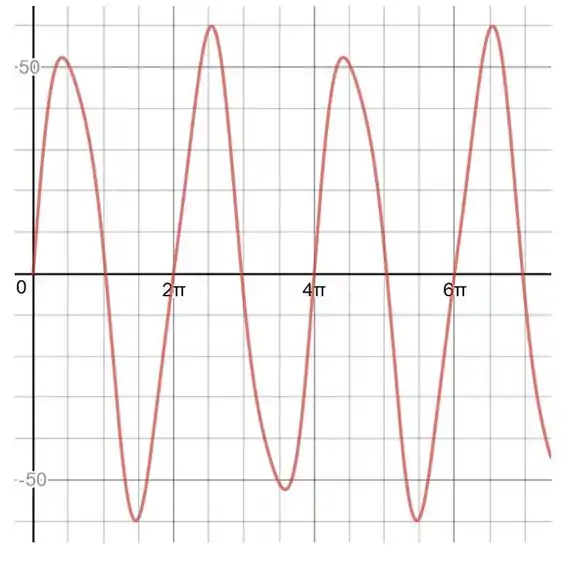
Passo 3
Desenhando os gráficos das trajetórias, no plano :
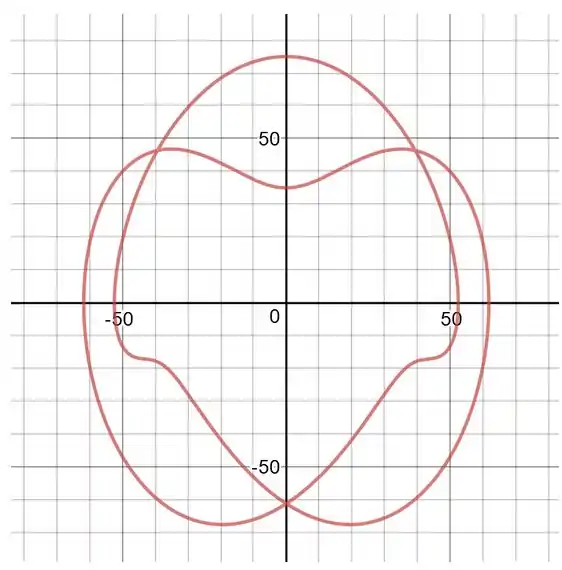
Temos também a trajetória no plano :
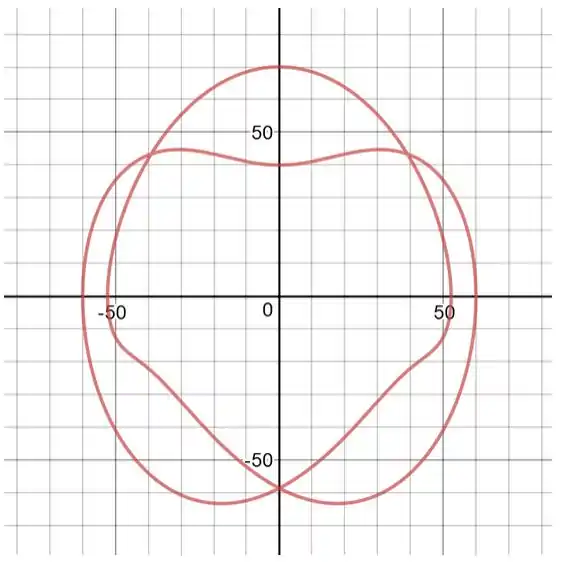
Resposta
E um período de