Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 5.3 - Ex. 24b
O polinômio de Legendre é definido como a solução polinomial da equação de Legendre
com que satisfaz, também, a condição .
a) Usando os resultados do Problema 23, encontre os polinômios de Legendre .
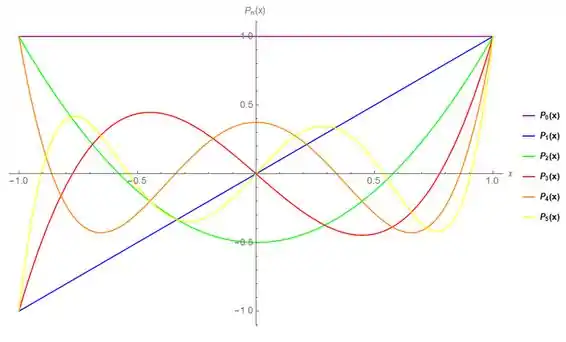
b) Faça os gráficos de para .
c) Encontre os zeros de .
Passo 1
b)Utilizando os cálculos que efetuamos no item (a) temos o s polinômios de Legendre e podemos desenhar sua funções.
Eu neste caso utilizei um software, mas caso você preferir efetuar na mão fique a vontade.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos problemas 23-34, mostre que as raízes indiciais diferem por um inteiro. Use o método de Frobenius para obter duas soluções seriais linearmente independentes em torno da singularidade regular x 0 =
Nos problemas 11-22, mostre que as raízes indiciais não diferem por um inteiro. Use o método de Frobenius para obter duas soluções seriais linearmente independentes em torno do ponto singular regular
Nos problemas 11-22, mostre que as raízes indiciais não diferem por um inteiro. Use o método de Frobenius para obter duas soluções seriais linearmente independentes em torno do ponto singular regular
Nos problemas 11-22, mostre que as raízes indiciais não diferem por um inteiro. Use o método de Frobenius para obter duas soluções seriais linearmente independentes em torno do ponto singular regular
Nos problemas 23-34, mostre que as raízes indiciais diferem por um inteiro. Use o método de Frobenius para obter duas soluções seriais linearmente independentes em torno da singularidade regular x 0 =